实验一：基于两阶段归并排序的集合运算

一、实验题目

实验目标

通过实现该任务，综合掌握数据从磁盘存储、缓冲区划分、磁盘到缓冲区的I/O操作及对应的集合运算处理流程。

实验要求

1. 编程语言不限，只要实现功能流程即可，不限制界面要求等；
2. 要求实现两种及两种以上的算法，可以从集合交、并、差、排序、去重复等操作中选取；
3. 功能上要求有模拟缓冲区设置、模拟磁盘元组数据分块存储、模拟磁盘I/O输入输出、模拟缓冲区运算四个基本功能；
4. 元组数据模拟过程中可以用整数型数据来模拟数据库元组内容（便于排序和集合操作）。

二、实现

本实验实现了排序和去重操作。

1. 分析

假设有 M 个内存缓冲区来进行排序，每个缓冲区的大小为 S 个元组，一个关系 R 被划分为 U 个子表，每个子表有 N 个块，每个块有 T 个元组，接下来，通过两个阶段对这个关系 R 进行排序。

在本程序中令 N = M，T = S，即每个缓冲区恰好存放一个块，且 M 个缓冲区恰好存放 N 个块，即一个子表，方便阶段 1 中对子表的元组进行排序，和阶段 2 中对所有子表进行归并（前提是子表数量不超过 M - 1，有一个缓冲区要作为输出缓冲区）

阶段1：排序每个子表

遍历每个子表：

1. 将子表中的所有元组分配到M个内存缓冲区中
2. 将M个缓冲区视为整体，对该范围内的整个子表进行排序（这里使用c++自带的sort函数）
3. 将排序后的子表写入磁盘

阶段2：归并排好序的子表

1. 初始化M-1个输入缓冲区和1个输出缓冲区
2. 在每个输入缓冲区中，加载每个子表内的第一个块
3. 在M-1个输入缓冲区中的第一个元组之间进行比较，选出最小的元素，将其移到输出缓冲块内的尾部
4. 如果输出缓冲块已满，则将其写入磁盘，并将输出缓冲区重新初始化
5. 如果某个输入缓冲区中的元组已经耗尽，则加载该输入缓冲区所装载子表内的下一个块，若无下一个块，则保持为空，不参与下次比较
6. 重复步骤3至5，直到所有输入缓冲区都为空
7. 将输出缓冲区中的剩余元素写入磁盘

去重操作

只需要记录上个输出到输出缓冲区的元素与当前准备输出的元素是否相同，若相同则销毁。

// 若 de 为 true 则开启去重模式
if (de && prev != min_tuple) {
    output_buffer.push(min_tuple);
}
else if (!de) output_buffer.push(min_tuple);
input_buffers[min_buffer_index].pop();
prev = min_tuple;

2. 实验结果

代码和详细注释

#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;

const int BUFFER_NUM = 6;    // 每个子表的块数量（也是缓冲区的数量）
const int BUFFER_SIZE = 5;   // 每个块的元组数（这里为方便，也作为缓冲区的大小）
const int MAX_SUBTABLES = BUFFER_NUM - 1;    // 定义子表的最大数量
typedef int Tuple;  // 定义元组类型为整型
bool de = false;

// 阶段1：排序子表写入外存
void phase1(vector<Tuple>& R, vector<vector<Tuple>>& sR) {
    // 每个子表的元组数
    int tuple_per_subtable = BUFFER_NUM * BUFFER_SIZE;

    cout << "============================ 排序子表 ============================" << endl;
    // 对每个子表进行排序并写入外存
    for (int l = 0, r = 0; l < R.size(); l = r) {
        cout << "------ 子表 " << l / tuple_per_subtable + 1 << " 全部输入到缓冲区进行排序------" << endl;
        cout << "排序前: " << endl;

        // 划分出子表范围，模拟输入到缓冲区
        r = min(l + tuple_per_subtable, (int)R.size());
        for (int i = l; i < r; ++i) cout << R[i] << " ";
        cout << endl;

        auto be = R.begin() + l, ed = R.begin() + r;
        sort(be, ed);

        cout << "排序后: " << endl;
        for (int i = l; i < r; ++i) cout << R[i] << " ";
        cout << endl;

        // 模拟缓冲区输出，写入外存
        vector<Tuple> origin(be, ed);
        sR.push_back(origin);
    }
}

// 阶段2：归并子表
void phase2(vector<vector<Tuple>>& sR, vector<Tuple>& ssR) {
    cout << "============================ 归并开始 ============================" << endl;
    // 输入缓冲区
    vector<queue<Tuple>> input_buffers(MAX_SUBTABLES);
    // 输出缓冲区
    queue<Tuple> output_buffer;
    // 记录每个子表中当前装入缓冲区的块号
    vector<int> sub_block_index(sR.size(), 0);
    // 记录上一个元组
    Tuple prev = INT_MAX;

    // 初始化输入缓冲区，i：子表编号，j：子表内元组编号
    for (int i = 0; i < sR.size(); ++i) {
        for (int j = 0; j < BUFFER_SIZE && j < sR[i].size(); ++j) {
            input_buffers[i].push(sR[i][j]);
        }
    }

    int count = 0;
    // 归并子表
    while (true) {
        // 从输入缓冲区中选择最小的元素，将其移到输出缓冲区中
        Tuple min_tuple = INT_MAX;
        int min_buffer_index = -1;

        // 找出最小的元组 min_tuple 所在的缓冲区 i
        for (int i = 0; i < input_buffers.size(); ++i) {
            if (!input_buffers[i].empty() && input_buffers[i].front() < min_tuple) {
                min_tuple = input_buffers[i].front();
                min_buffer_index = i;
            }
        }

        if (min_buffer_index == -1) {
            cout << "输入缓冲区已清空。" << endl;
            break;
        }

        // 将最小的元组转移到输出缓冲区
        if (de && prev != min_tuple) {
            output_buffer.push(min_tuple);
        }
        else if (!de) output_buffer.push(min_tuple);
        input_buffers[min_buffer_index].pop();
        prev = min_tuple;

        // 如果输出缓冲区已满，将其写入外存并清空
        if (output_buffer.size() >= BUFFER_SIZE) {
            cout << "输出缓冲区满，向磁盘写入数据块(" << ++count << ")：";
            // 这里模拟将输出缓冲区写入外存
            while (!output_buffer.empty()) {
                Tuple toWrite = output_buffer.front();
                output_buffer.pop();
                ssR.push_back(toWrite);
                cout << toWrite << ' ';
            }
            cout << endl;
        }

        // 如果某个输入缓冲区已清空，加载下一个子表
        if (input_buffers[min_buffer_index].empty()) {
            int block_index = ++sub_block_index[min_buffer_index];
            int be_index = block_index * BUFFER_SIZE;    // 要装入的元组起始编号
            int ed_index = min(be_index + BUFFER_SIZE, (int)sR[min_buffer_index].size());   // 要装入的元组终止编号 + 1
            
            // 复制下一个块的元素到输入缓冲区
            for (int i = be_index; i < ed_index; ++i) {
                input_buffers[min_buffer_index].push(sR[min_buffer_index][i]);
            }
        }
    }

    // 处理输出缓冲区中剩余的元素
    cout << "将输出缓冲区剩余元素写入磁盘：";
    while (!output_buffer.empty()) {
        Tuple toWrite = output_buffer.front();
        output_buffer.pop();
        ssR.push_back(toWrite);
        cout << toWrite << ' ';
    }
    cout << endl;
    cout << "============================ 归并完成 ============================" << endl;
}

// 初始化关系 R
void initialize_R(vector<Tuple>& R, int tuple_num) {
    // 设置随机种子
    srand(time(nullptr));

    // 随机生成元组并填充关系 R
    for (int i = 0; i < tuple_num; ++i) {
        // 生成随机数作为元组的值
        Tuple value = rand() % 1000; // 取值范围是0到999
        R.push_back(value);
    }
}

void print(vector<Tuple>& r) {
    for (auto it = r.begin(); it != r.end(); ++it)
        cout << *it << ' ';
    cout << endl;
}

int main() {
    cout << "==================================================================" << endl;
    int block_num;  // 关系 R 拥有的块数量
    int tuple_num;
    int subtable_num;   // 子表数量
    int max_tuple = MAX_SUBTABLES * BUFFER_NUM * BUFFER_SIZE;

    while (true) {
        cout << "是否要进行去重操作：1.是  2.否  回答：";
        int ans;
        cin >> ans;
        if (ans == 1) {
            de = true;
            break;
        }
        else if (ans == 2) {
            de = false;
            break;
        }
    }

    while (true) {
        cout << "不能超过 " << max_tuple << " 个元组。" << endl;
        cout << "请输入元组总数：";
        cin >> tuple_num;
        block_num = ceil((double)tuple_num / BUFFER_SIZE);
        subtable_num = ceil((double)block_num / BUFFER_NUM);
        if (tuple_num <= max_tuple) {
            cout << "创建成功，当前关系 R 有 " << subtable_num << " 个字表，";
            cout << "每个子表有 " << BUFFER_NUM << " 个块，每块有 " << BUFFER_SIZE << " 个元组。" <<  endl;
            break;
        }
        cout << "生成子表过多，创建失败。" << endl;
    }

    vector<Tuple> R;    // 初始关系 R
    vector<vector<Tuple>> sR;    // 每个子表排序后的关系 R
    vector<Tuple> ssR; // 完全排序后的关系 R

    // 定义一个关系 R，里面总共有 block_num 个块，subtable_num 个子表，每个子表有 SUBTABLES_BLOCK_NUM 个块（最后一个子表可能没有）
    // 每个块有 BUFFER_SIZE 个元素，关系 R 一共有 block_num * BUFFER_SIZE 个元素
    initialize_R(R, tuple_num);

    cout << "初始元素：" << endl;;
    print(R);

    // 阶段1：将子表写入外存并排序
    phase1(R, sR);

    // 阶段2：归并子表
    phase2(sR, ssR);

    cout << "排序后元素：" << endl;;
    print(ssR);

    cout << "==================================================================" << endl;
    return 0;
}

控制台输出

==================================================================
是否要进行去重操作：1.是  2.否  回答：1
不能超过 150 个元组。
请输入元组总数：53
创建成功，当前关系 R 有 2 个字表，每个子表有 6 个块，每块有 5 个元组。
初始元素：
894 852 768 884 545 194 995 34 361 805 931 542 740 277 986 289 600 211 431 327 223 499 187 590 401 484 723 527 288 66 485 692 2 301 854 267 338 35 451 10 64 116 262 451 154 109 836 914 867 143 973 21 740
============================ 排序子表 ============================
------ 子表 1 全部输入到缓冲区进行排序------
排序前:
894 852 768 884 545 194 995 34 361 805 931 542 740 277 986 289 600 211 431 327 223 499 187 590 401 484 723 527 288 66
排序后:
34 66 187 194 211 223 277 288 289 327 361 401 431 484 499 527 542 545 590 600 723 740 768 805 852 884 894 931 986 995
------ 子表 2 全部输入到缓冲区进行排序------
排序前:
485 692 2 301 854 267 338 35 451 10 64 116 262 451 154 109 836 914 867 143 973 21 740
排序后:
2 10 21 35 64 109 116 143 154 262 267 301 338 451 451 485 692 740 836 854 867 914 973
============================ 归并开始 ============================
输出缓冲区满，向磁盘写入数据块(1)：2 10 21 34 35
输出缓冲区满，向磁盘写入数据块(2)：64 66 109 116 143
输出缓冲区满，向磁盘写入数据块(3)：154 187 194 211 223
输出缓冲区满，向磁盘写入数据块(4)：262 267 277 288 289
输出缓冲区满，向磁盘写入数据块(5)：301 327 338 361 401
输出缓冲区满，向磁盘写入数据块(6)：431 451 484 485 499
输出缓冲区满，向磁盘写入数据块(7)：527 542 545 590 600
输出缓冲区满，向磁盘写入数据块(8)：692 723 740 768 805
输出缓冲区满，向磁盘写入数据块(9)：836 852 854 867 884
输出缓冲区满，向磁盘写入数据块(10)：894 914 931 973 986
输入缓冲区已清空。
将输出缓冲区剩余元素写入磁盘：995
============================ 归并完成 ============================
排序后元素：
2 10 21 34 35 64 66 109 116 143 154 187 194 211 223 262 267 277 288 289 301 327 338 361 401 431 451 484 485 499 527 542 545 590 600 692 723 740 768 805 836 852 854 867 884 894 914 931 973 986 995
==================================================================

实验二：B-树实验

一、实验题目

实验目标

通过实现该任务，掌握B-树的结构，并实现建立、插入、删除等操作。

实验要求

1. 编程语言不限，只要实现功能流程即可，不限制界面要求等；
2. 要求实现建立、插入、删除三种操作；
3. 可以通过整数型数据来模拟键值，具体的指针可以不用涉及；
4. 能够体现操作变化过程最好，至少体现操作的结果。

二、实现

1. 分析

函数图

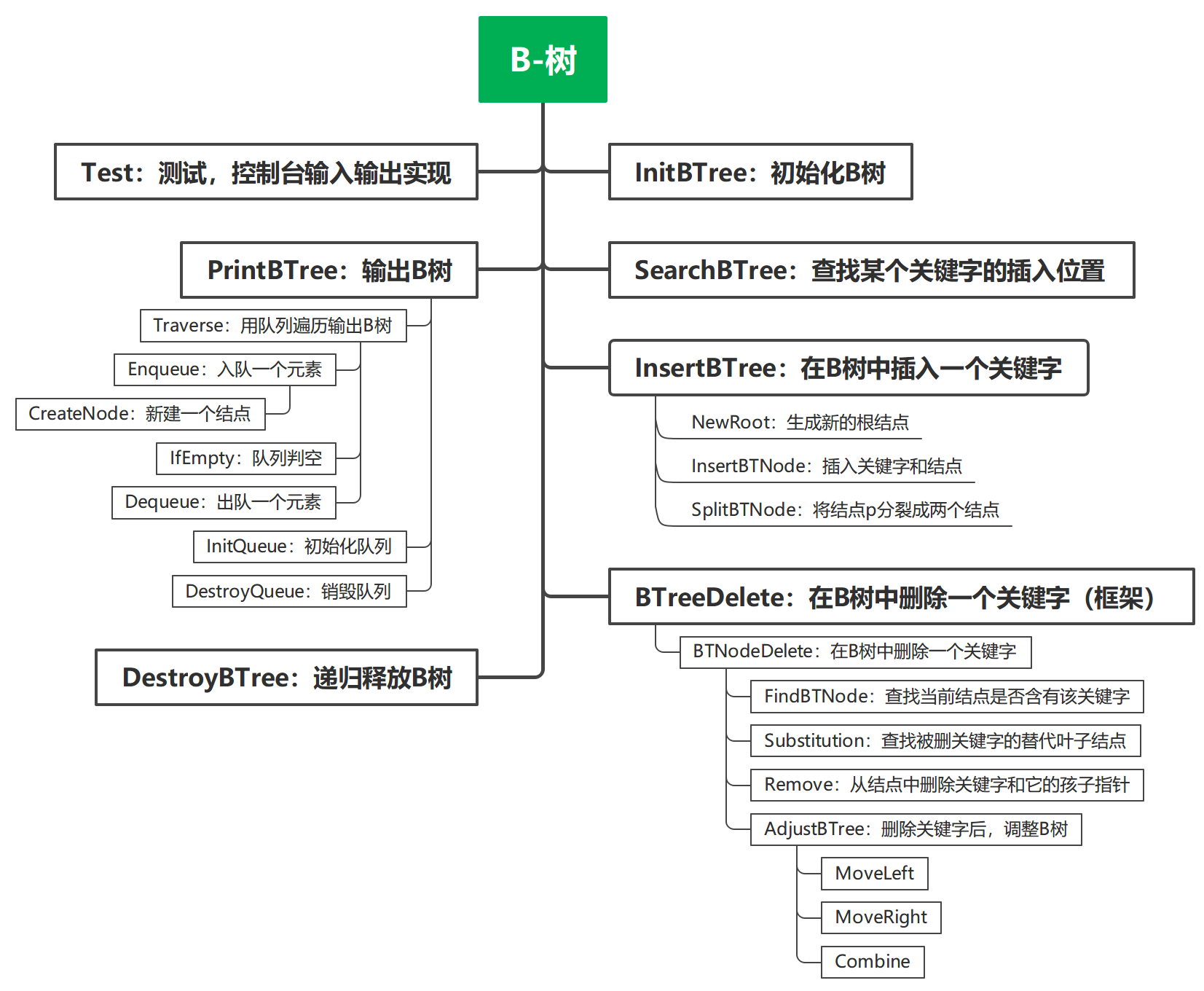
关键操作的流程

a. 插入

1. SearchBTree 函数在树上查找关键字 k，若查找成功，则特征值 tag = 1，返回 pt 结点以及关键字对应的编号 i；否则特征值 tag = 0，返回关键字 k 应该插入的位置
2. 通过 InsertBTree 函数开始插入操作，该函数接受B树的根节点指针 t、待插入的关键字 k 、SearchBTree 函数返回的待插入位置 i和指向待插入位置的节点指针 p
3. 如果 B 树为空树（即根节点为空），则调用 NewRoot 函数生成一个仅含有关键字 k 的根节点
4. 如果 B 树不为空，则进行以下步骤：
   • 将关键字 k 插入到节点 p 的关键字数组中的第 i + 1 个位置，同时将指向待插入位置的子节点指针 q 插入到节点 p 的孩子节点数组中的第 i + 1 个位置，调用 InsertBTNode 函数实现
   • 如果节点 p 中关键字数量未超过最大阶数，则插入操作完成
   • 如果节点 p 中关键字数量已经达到最大阶数，则需要进行节点分裂：
     • 首先，调用 SplitBTNode 函数将节点 p 分裂为两个节点 p 和 q，其中 p 保留前一半关键字，q 移入后一半关键字
     • 然后，将分裂后的中位数关键字 x 移动到父节点中，并将原节点 p 的父节点作为新节点 p，循环进行此过程直至找到插入位置
     • 如果达到根节点，但根节点也已满，则调用 NewRoot 函数生成新的根节点，并将原根节点和新分裂出的节点作为子节点连接到新根节点上

b. 删除

1. 删除关键字操作：

   • 首先，通过 BTNodeDelete 函数开始删除操作，该函数接受一个节点指针 p 和待删除的关键字 k
   • 在该函数中，首先调用 FindBTNode 函数查找待删除关键字的位置 i，如果关键字存在，则返回1，否则返回0
   • 如果关键字存在，进一步判断：
     • 如果待删除关键字所在节点 p 的子节点不为空，则说明待删除关键字是非叶子节点，此时调用 Substitution 函数寻找右子树中最小的关键字替代待删除关键字，并递归调用 BTNodeDelete 函数删除右子树中最小的关键字
     • 如果待删除关键字所在节点 p 的子节点为空，则说明待删除关键字是叶子节点，直接调用 Remove 函数从节点中删除该关键字
   • 删除完成后，检查当前节点关键字数量是否小于最小阶数，如果是，则调用 AdjustBTree 函数进行B树的调整。

2. 节点删除和调整：

   • Remove 函数实现了删除节点中的关键字和子节点的操作，通过前移来删除关键字和子节点

   • Substitution 函数用于在删除非叶子节点的情况下寻找右子树中最小的关键字替代待删除关键字

   • MoveRight、MoveLeft 和 Combine 函数用于节点合并和关键字移动的操作

     代码中有详细注解

   • AdjustBTree 函数用于调整B树结构，根据删除位置和兄弟节点的关键字数量来决定是否进行关键字移动、节点合并或者继续调整父节点

3. 根节点调整：

   • 如果删除操作后根节点的关键字数量为0，则说明根节点已经被删除，此时需要调整根节点指针，将新的根节点指向原根节点的子节点

4. 整体删除操作：

   • 在 BTreeDelete 函数中，接收 BTNodeDelete 函数的返回值（是否查找到需要删除的关键字），如果查找失败，则输出提示信息；如果查找成功（删除成功），则继续检查根节点是否需要调整；如果根节点为空，则释放原根节点的空间并更新根节点指针

2. 实验结果

代码和详细注释

b-tree.h

#ifndef _BTREE_H
#define _BTREE_H
#define MAXM 10     // B树的最大阶数

const int M = 4;                // 设定B树的阶数
const int Max = M - 1;          // 结点的最大关键字数量
const int Min = (M - 1) / 2;    // 结点的最小关键字数量
typedef int KeyType;            // KeyType表示关键字类型，这里为整型

// B树和B树结点类型
typedef struct Node {
    int keynum;         // 结点关键字个数
    KeyType key[MAXM];  // 关键字数组，key[0]不使用
    struct Node* parent;    // 双亲结点指针
    struct Node* child[MAXM]; // 孩子结点指针数组
}BTNode, *BTree;

// B树查找结果
typedef struct {                    
    BTNode* pt; // 指向找到的结点
    int i;      // 在结点中的关键字位置; 
    int tag;    // 查找成功与否标志
}Result;

// 链表
typedef struct LNode {
    BTree data;
    struct LNode* next;
}LNode, *LinkList;

// 枚举状态
typedef enum status {
    TRUE,
    FALSE,
    OK,
    ERROR,
    OVER_FLOW,
    EMPTY
}Status;

/* 初始化B树 */
Status InitBTree(BTree& t);

/* 在树 t 上查找关键字 k，返回结果 (pt, i, tag)。
   若查找成功，则特征值 tag = 1，返回 pt 结点以及关键字对应的编号 i；
   否则特征值 tag = 0，返回关键字 k 应该插入的位置为 pt 结点的第 i 个 */
Result SearchBTree(BTree t, KeyType k);

/* 将关键字 k 和结点 q 分别插入到 p->key[i+1] 和 p->child[i+1] 中 */
void InsertBTNode(BTNode*& p, int i, KeyType k, BTNode* q);       

/* 将结点 p 分裂成两个结点，前一半保留，后一半移入结点 q */
void SplitBTNode(BTNode*& p, BTNode*& q);                    

/* 生成新的根结点 t，原结点 p 和结点 q 为子树指针 */
void NewRoot(BTNode*& t, KeyType k, BTNode* p, BTNode* q);      

/* 在树 t 上结点 p 的 key[i] 与 key[i+1] 之间插入关键字 k。若引起结点过大，则沿双亲链进行必要的结点分裂调整，使 t 仍是B树 */
void InsertBTree(BTree& t, int i, KeyType k, BTNode* p);

/* 从 p 结点删除 key[i] 和它的孩子指针 child[i] */
void Remove(BTNode* p, int i);

/* 查找被删关键字 p->key[i](在非叶子结点中)的替代叶子结点(右子树中值最小的关键字) */
void Substitution(BTNode* p, int i);

/* 将双亲结点 p 中的最后一个关键字移入右结点 q 中，将左结点 aq 中的最后一个关键字移入双亲结点 p 中*/
void MoveRight(BTNode* p, int i);

/* 将双亲结点p中的第一个关键字移入结点 aq 中，将结点 q 中的第一个关键字移入双亲结点 p 中 */
void MoveLeft(BTNode* p, int i);

/* 将双亲结点 p、右结点 q 合并入左结点 aq，并调整双亲结点 p 中的剩余关键字的位置 */
void Combine(BTNode* p, int i);

/* 删除结点 p 中的第 i 个关键字后，调整B树 */
void AdjustBTree(BTNode* p, int i);

/* 反映是否在结点p中是否查找到关键字k */
int FindBTNode(BTNode* p, KeyType k, int& i);

/* 在结点 p 中查找并删除关键字 k */
int BTNodeDelete(BTNode* p, KeyType k);

/* 构建删除框架，执行删除操作 */
void BTreeDelete(BTree& t, KeyType k);

/* 递归释放B树 */
void DestroyBTree(BTree& t);

/* 初始化队列 */
Status InitQueue(LinkList& L);

/* 新建一个结点 */
LNode* CreateNode(BTNode* p);

/* 元素 q 入队列 */
Status Enqueue(LNode* p, BTNode* q);

/* 出队列，并以 q 返回值 */
Status Dequeue(LNode* p, BTNode*& q);

/* 队列判空 */
Status IfEmpty(LinkList L);

/* 销毁队列 */
void DestroyQueue(LinkList L);

/* 用队列遍历输出B树 */
Status Traverse(BTree t, LinkList L, int newline, int sum);

/* 输出B树 */
Status PrintBTree(BTree t);

/* 测试 */
void Test();

#endif

b-tree.cpp

#include <iostream>
#include "b-tree.h"
using namespace std;

Status InitBTree(BTree& t) {
    //初始化B树 
    t = NULL;
    return OK;
}

Result SearchBTree(BTree t, KeyType k) {
    BTNode* p = t, * q = NULL;  // p 指向待查结点，q 指向 p 的双亲
    int found_tag = 0;  // 设定查找成功与否标志
    int i = 0;
    Result r;   // 设定返回的查找结果

    // 遍历每个结点
    while (p != NULL && found_tag == 0) {
        // 在结点 p 中查找关键字 k ，使得 p->key[i] <= k < p->key[i+1]
        for (i = 0; i < p->keynum && p->key[i + 1] <= k; i++);

        // 查找成功
        if (i > 0 && p->key[i] == k)
            found_tag = 1;
        // 查找失败
        else {
            q = p;
            p = p->child[i];
        }
    }

    r.pt = (found_tag == 1) ? p : q;
    r.i = i;
    r.tag = found_tag;
    return r;   // 返回关键字k的位置(或插入位置)
}

void InsertBTNode(BTNode*& p, int i, KeyType k, BTNode* q) {
    int j;
    // 整体后移空出一个位置
    for (j = p->keynum; j > i; j--) {
        p->key[j + 1] = p->key[j];
        p->child[j + 1] = p->child[j];
    }
    p->key[i + 1] = k;
    p->child[i + 1] = q;
    if (q != NULL)
        q->parent = p;
    p->keynum++;
}

void SplitBTNode(BTNode*& p, BTNode*& q) {
    int i;
    int s = (M + 1) / 2;
    q = (BTNode*)malloc(sizeof(BTNode));             //给结点q分配空间

    // 原结点的后一半关键字以及子节点都移入结点 q
    q->child[0] = p->child[s];  // 最左边的孩子结点指针单独设置一下，因为它没有对应的左区间关键字
    for (i = s + 1; i <= M; i++) {
        q->key[i - s] = p->key[i];
        q->child[i - s] = p->child[i];
    }
    q->keynum = p->keynum - s;
    q->parent = p->parent;

    // 修改子结点的双亲指针
    for (i = 0; i <= p->keynum - s; i++)
        if (q->child[i] != NULL)
            q->child[i]->parent = q;

    p->keynum = s - 1;  // 结点 p 的前一半保留，修改结点 p 的 keynum
}

void NewRoot(BTNode*& t, KeyType k, BTNode* p, BTNode* q) {
    t = (BTNode*)malloc(sizeof(BTNode));             //分配空间 
    t->keynum = 1;
    t->child[0] = p;
    t->child[1] = q;
    t->key[1] = k;
    if (p != NULL)                                     //调整结点p和结点q的双亲指针 
        p->parent = t;
    if (q != NULL)
        q->parent = t;
    t->parent = NULL;
}

void InsertBTree(BTree& t, int i, KeyType k, BTNode* p) {
    BTNode* q;
    KeyType x;
    // 如果 t 是空树
    if (p == NULL)
        NewRoot(t, k, NULL, NULL);  // 生成仅含关键字 k 的根结点 t
    // 如果 t 不为空
    else {
        x = k;
        q = NULL;

        while (true) {
            InsertBTNode(p, i, x, q);   // 将关键字 x 和结点 q 分别插入到 p->key[i+1] 和 p->child[i+1] 中
            if (p->keynum <= Max)
                break;  // 没满，不需要继续分裂了，插入完成
            else {
                int s = (M + 1) / 2;    // s 为留在当前结点的关键字数，剩下的 keynum - s 个关键字都移动到新的兄弟结点
                SplitBTNode(p, q);  // 分裂结点
                x = p->key[s];  // x 为中位数，移动到父亲结点去

                // 查找 x 的插入位置
                if (p->parent) {
                    p = p->parent;
                    for (i = 0; i < p->keynum && p->key[i + 1] <= k; i++);
                }
                // 如果没有双亲结点存放 x，就需要新建一个了，但此时也不需要继续分裂了，因为父结点不可能再满，故跳出循环
                else {
                    NewRoot(t, x, p, q);    // 生成新根结点 t，p 和 q 为子树指针
                    break;
                }
            }
        }
    }
}

void Remove(BTNode* p, int i) {
    int j;
    // 前移删除 key[i] 和 child[i]
    for (j = i + 1; j <= p->keynum; j++) {
        p->key[j - 1] = p->key[j];
        p->child[j - 1] = p->child[j];
    }
    p->keynum--;
}

void Substitution(BTNode* p, int i) {
    BTNode* q;
    for (q = p->child[i]; q->child[0] != NULL; q = q->child[0]);
    p->key[i] = q->key[1];  //复制关键字值
}

void MoveRight(BTNode* p, int i) {
    int j;
    BTNode* q = p->child[i];
    BTNode* aq = p->child[i - 1];

    // 将右兄弟 q 中所有关键字向后移动一位
    for (j = q->keynum; j > 0; j--) {
        q->key[j + 1] = q->key[j];
        q->child[j + 1] = q->child[j];
    }

    // 从双亲结点 p 移动关键字到右兄弟 q 中
    q->child[1] = q->child[0];
    q->key[1] = p->key[i];
    q->keynum++;

    // 将左兄弟 aq 中最后一个关键字移动到双亲结点 p 中
    p->key[i] = aq->key[aq->keynum];
    p->child[i]->child[0] = aq->child[aq->keynum];
    aq->keynum--;
}

void MoveLeft(BTNode* p, int i) {
    int j;
    BTNode* aq = p->child[i - 1];
    BTNode* q = p->child[i];

    // 把双亲结点 p 中的关键字移动到左兄弟 aq 中
    aq->keynum++;                                   
    aq->key[aq->keynum] = p->key[i];
    aq->child[aq->keynum] = p->child[i]->child[0];

    // 把右兄弟 q 中的关键字移动到双亲节点 p 中
    p->key[i] = q->key[1];                            
    q->child[0] = q->child[1];
    q->keynum--;

    // 将右兄弟 q 中所有关键字向前移动一位
    for (j = 1; j <= q->keynum; j++) {                     
        q->key[j] = q->key[j + 1];
        q->child[j] = q->child[j + 1];
    }
}

void Combine(BTNode* p, int i) {
    int j;
    BTNode* q = p->child[i];
    BTNode* aq = p->child[i - 1];

    // 将双亲结点的关键字 p->key[i] 插入到左结点 aq
    aq->keynum++;
    aq->key[aq->keynum] = p->key[i];
    aq->child[aq->keynum] = q->child[0];

    // 将右结点 q 中的所有关键字插入到左结点 aq 
    for (j = 1; j <= q->keynum; j++) {
        aq->keynum++;
        aq->key[aq->keynum] = q->key[j];
        aq->child[aq->keynum] = q->child[j];
    }

    // 将双亲结点 p 中的 p->key[i] 后的所有关键字向前移动一位
    for (j = i; j < p->keynum; j++) {
        p->key[j] = p->key[j + 1];
        p->child[j] = p->child[j + 1];
    }
    p->keynum--;    // 修改双亲结点 p 的 keynum 值 
    free(q);    // 释放空右结点q的空间
}

void AdjustBTree(BTNode* p, int i) {
    // 如果删除的是最左边关键字
    if (i == 0) {
        if (p->child[1]->keynum > Min)  //右结点可以借
            MoveLeft(p, 1);
        else    //右兄弟不够借 
            Combine(p, 1);
    }
    // 如果删除的是最右边关键字
    else if (i == p->keynum) {
        if (p->child[i - 1]->keynum > Min)  //左结点可以借 
            MoveRight(p, i);
        else    //左结点不够借 
            Combine(p, i);
    }
    // 如果删除关键字在中部且左结点够借 
    else if (p->child[i - 1]->keynum > Min) {
        MoveRight(p, i);
    }
    // 如果删除关键字在中部且右结点够借 
    else if (p->child[i + 1]->keynum > Min) {
        MoveLeft(p, i + 1);
    }
    // 如果删除关键字在中部且左右结点都不够借
    else {
        Combine(p, i);
    }
}

int FindBTNode(BTNode* p, KeyType k, int& i) {
    // 结点 p 中查找关键字 k 失败 
    if (k < p->key[1]) {
        i = 0;
        return 0;
    }
    // 在 p 结点中查找
    else {
        i = p->keynum;
        while (k < p->key[i] && i>1)
            i--;
        // 结点 p 中查找关键字 k 成功
        if (k == p->key[i])
            return 1;
    }
}

int BTNodeDelete(BTNode* p, KeyType k) {
    int i;
    int found_tag;  // 查找标志 
    if (p == NULL)
        return 0;
    else {
        found_tag = FindBTNode(p, k, i);    // 返回查找结果
        // 查找成功 
        if (found_tag == 1) {
            // 删除的是非叶子结点
            if (p->child[i - 1] != NULL) {
                Substitution(p, i);     // 寻找相邻关键字(右子树中最小的关键字) 
                BTNodeDelete(p->child[i], p->key[i]);   // 执行删除操作 
            }
            else
                Remove(p, i);   // 从结点 p 中位置 i 处删除关键字
        }
        else
            found_tag = BTNodeDelete(p->child[i], k);   // 沿孩子结点递归查找并删除关键字 k
        if (p->child[i] != NULL)
            if (p->child[i]->keynum < Min)  // 删除后关键字个数小于 Min
                AdjustBTree(p, i);  // 调整B树 
        return found_tag;
    }
}

void BTreeDelete(BTree& t, KeyType k) {
    BTNode* p;
    int a = BTNodeDelete(t, k); // 删除关键字k 
    // 查找失败
    if (a == 0)
        cout << "   关键字" << k << "不在B树中" << endl;
    //调整
    else if (t->keynum == 0) {
        p = t;
        t = t->child[0];
        free(p);
    }
}

void DestroyBTree(BTree& t) {
    int i;
    BTNode* p = t;
    // 如果B树不为空  
    if (p != NULL) {
        // 递归释放每一个结点 
        for (i = 0; i <= p->keynum; i++) {
            DestroyBTree(*&p->child[i]);
        }
        free(p);
    }
    t = NULL;
}

Status InitQueue(LinkList& L) {
    L = (LNode*)malloc(sizeof(LNode));  // 分配结点空间 
    if (L == NULL)  // 分配失败              
        return OVER_FLOW;
    L->next = NULL;
    return OK;
}

LNode* CreateNode(BTNode* p) {
    LNode* q;
    q = (LNode*)malloc(sizeof(LNode));  // 分配结点空间
    if (q != NULL) {    // 分配成功 
        q->data = p;
        q->next = NULL;
    }
    return q;
}

Status Enqueue(LNode* p, BTNode* q) {
    if (p == NULL)
        return ERROR;
    while (p->next != NULL)     // 调至队列最后 
        p = p->next;
    p->next = CreateNode(q);    // 生成结点让q进入队列 
    return OK;
}

Status Dequeue(LNode* p, BTNode*& q) {
    LNode* aq;
    if (p == NULL || p->next == NULL)   // 删除位置不合理 
        return ERROR;
    aq = p->next;   // 修改被删结点aq的指针域
    p->next = aq->next;
    q = aq->data;
    free(aq);   // 释放结点aq
    return OK;
}

Status IfEmpty(LinkList L) {
    if (L == NULL)  // 队列不存在 
        return ERROR;
    if (L->next == NULL)    // 队列为空 
        return TRUE;
    return FALSE;   // 队列非空 
}

void DestroyQueue(LinkList L) {
    LinkList p;
    if (L != NULL) {
        p = L;
        L = L->next;
        free(p);    // 逐一释放 
        DestroyQueue(L);
    }
}

Status Traverse(BTree t, LinkList L, int newline, int sum) {
    int i;
    BTree p;
    if (t != NULL) {
        cout << "  [";
        Enqueue(L, t->child[0]);    // 入队
        for (i = 1; i <= t->keynum; i++) {
            cout << ' ' << t->key[i] << ' ';
            Enqueue(L, t->child[i]);    // 子结点入队
        }
        sum += t->keynum + 1;
        cout << "]";
        if (newline == 0) {     // 需要另起一行
            cout << endl;
            newline = sum - 1;
            sum = 0;
        }
        else
            newline--;
    }

    if (IfEmpty(L) == FALSE) {  // l不为空
        Dequeue(L, p);  // 出队，以p返回
        Traverse(p, L, newline, sum);   // 遍历出队结点
    }
    return OK;
}

Status PrintBTree(BTree t) {
    LinkList L;
    if (t == NULL) {
        cout << "  [ 空 ]" << endl;
        return OK;
    }
    InitQueue(L);   // 初始化队列
    Traverse(t, L, 0, 0);   // 利用队列输出
    DestroyQueue(L);    // 销毁队列
    return OK;
}

void Test() {
    int i, k;
    BTree t = NULL;
    Result s;   // 定义查找结果

    while (1) {
        cout << " 此时的B树：" << endl;
        PrintBTree(t);
        cout << "" << endl;
        cout << "=======================================================" << endl;
        cout << "   1.初始化     2.插入    3.删除    4.清空    5.退出" << endl;
        cout << "=======================================================" << endl;
        cout << " 输入序号执行相应操作：";
        cin >> i;

        switch (i) {
        case 1:
        {
            InitBTree(t);
            cout << " 初始化完成。" << endl;
            break;
        }
        case 2:
        {
            cout << " 输入要插入的关键字：";
            cin >> k;
            s = SearchBTree(t, k);
            InsertBTree(t, s.i, k, s.pt);
            cout << " 插入成功。" << endl;
            break;
        }
        case 3:
        {
            cout << " 输入要删除的关键字：";
            cin >> k;
            BTreeDelete(t, k);
            cout << endl;
            cout << " 删除成功。" << endl;
            break;
        }
        case 4:
        {
            DestroyBTree(t);
            cout << " 已清空。" << endl;
            break;
        }
        case 5:
        {
            exit(-1);
            break;
        }
        }
    }
}

int main() {
    Test();
    return 0;
}

控制台输出

...

 此时的B树：
  [ 6  51  54 ]
  [ 4 ]  [ 7  8  12 ]  [ 52  53 ]  [ 123  234 ]

=======================================================
   1.初始化     2.插入    3.删除    4.清空    5.退出
=======================================================
 输入序号执行相应操作：2
 输入要插入的关键字：9
 插入成功。
 此时的B树：
  [ 8 ]
  [ 6 ]  [ 51  54 ]
  [ 4 ]  [ 7 ]  [ 9  12 ]  [ 52  53 ]  [ 123  234 ]

=======================================================
   1.初始化     2.插入    3.删除    4.清空    5.退出
=======================================================
 输入序号执行相应操作：3
 输入要删除的关键字：8

 删除成功。
 此时的B树：
  [ 9 ]
  [ 6 ]  [ 51  54 ]
  [ 4 ]  [ 7 ]  [ 12 ]  [ 52  53 ]  [ 123  234 ]

=======================================================
   1.初始化     2.插入    3.删除    4.清空    5.退出
=======================================================
 输入序号执行相应操作：4
 已清空。
 此时的B树：
  [ 空 ]

=======================================================
   1.初始化     2.插入    3.删除    4.清空    5.退出
=======================================================
 输入序号执行相应操作：5
 
 D:\CodeProjects\DBMSWORK\x64\Debug\work1.exe (进程 26748)已退出，代码为 -1。

实验三：构建语法分析树实验

一、实验题目

实验目标

通过实现该任务，综合掌握基于关系代数表达式的语法分析树构建过程及功能。

实验要求

1. 编程语言不限，只要实现功能流程即可，不限制界面要求等；
2. 输入一个完整的SQL查询语句，能够输出一个构建好的语法分析树；

二、实现

1. 分析

语法规则

这里使用书上的语法规则：

查询

<Query> ::= SELECT <SelList> FROM <FromList> WHERE <Condition>

选择列表

<SelList> ::= <Attribute>, <SelList> 
<SelList> ::= <Attribute>

from列表

<FromList> ::= <Relation>, <FromList> 
<FromList> ::= <Relation>

条件

<Condition> ::= <Condition> AND <Condition> 
<Condition> ::= <Attribute> IN (<Query>) 
<Condition> ::= <Attribute> = <Attribute> （实际实现了"<=", ">=", "=", "<", ">"）
<Condition> ::= <Attribute> LIKE <Pattern>

<Attribute>、<Relation>、<Pattern> 通过它们所代表的原子的规则定义。

流程

1. 定义语法分析树的结构

// 定义节点类型
enum class NodeType {
    QUERY,
    SEL_LIST,
    ATTRIBUTE,
    FROM_LIST,
    RELATION,
    CONDITION,
    PATTERN
};
// 节点结构体
struct Node {
    NodeType type;          // 节点类型
    string value;           // 节点值
    vector<Node> children;  // 子节点列表
};

2. 依次递归调用各自的解析器函数

1. 当节点类型为ATTRIBUTE、RELATION、PATTERN 时，它有节点值，没有子节点

2. 当节点类型为QUERY时，它没有节点值，有三个子节点SEL_LIST、FROM_LIST、CONDITION

3. 当节点类型为SEL_LIST时，它有1个或2个子节点。

   • 当它有1个子节点时，自身无节点值，子节点类型为ATTRIBUTE

   • 当它有2个子节点时，左节点类型为ATTRIBUTE，右节点类型为SEL_LIST（并递归下降解析下一层），其自身的节点值为 " , "

   节点类型为FROM_LIST时，同SEL_LIST

4. 当节点类型为CONDITION时，依次查找关键字 "AND", "IN", "= (以及其他比较符号)", "LIKE" ，将查找到的关键字作为节点值，并根据语法规则对左右子节点赋予相应的节点类型，然后对它们进行必要的递归下降解析

3. 打印输出语法分析树

树每下降一层，就增加一个缩进（4个空格），同一层节点缩进相同。根据不同的节点类型进行相应的处理，模仿书中语法树结构，打印输出。

2. 实验结果

代码和详细注释

#include <iostream>
#include <string>
#include <vector>
using namespace std;

// 定义节点类型
enum class NodeType {
    QUERY,
    SEL_LIST,
    ATTRIBUTE,
    FROM_LIST,
    RELATION,
    CONDITION,
    PATTERN
};

// 节点结构体
struct Node {
    NodeType type;          // 节点类型
    string value;           // 节点值
    vector<Node> children;  // 子节点列表
};

// 打印语法树
void printSyntaxTree(const Node& node, int level = 0) {
    // 打印缩进
    for (int i = 0; i < level; ++i) {
        cout << "    ";
    }

    // Query 入口，如果不是第一个 Query 则需要加括号
    if (node.type == NodeType::QUERY) {
        if (level) {
            cout << '(' << endl;
            for (int i = 0; i < level; ++i) cout << "    ";
        }

        cout << "<Query>" << endl;
        for (int i = 0; i <= level; ++i) cout << "    ";
        cout << "SELECT" << endl;
        printSyntaxTree(node.children[0], level + 1);
        for (int i = 0; i <= level; ++i) cout << "    ";
        cout << "FROM" << endl;
        printSyntaxTree(node.children[1], level + 1);
        for (int i = 0; i <= level; ++i) cout << "    ";
        cout << "WHERE" << endl;
        printSyntaxTree(node.children[2], level + 1);

        if (level) {
            for (int i = 0; i < level; ++i) cout << "    ";
            cout << ')' << endl;
        }
    }

    // 根据节点类型打印节点值
    switch (node.type) {
    case NodeType::SEL_LIST:
        cout << "<SelList>" << endl;
        printSyntaxTree(node.children[0], level + 1);
        if (!node.value.empty()) {
            for (int i = 0; i <= level; ++i) cout << "    ";
            cout << node.value << endl;
            printSyntaxTree(node.children[1], level + 1);
        }
        break;
    case NodeType::ATTRIBUTE:
        cout << "<Attribute>: " << node.value << endl;
        break;
    case NodeType::FROM_LIST:
        cout << "<FromList>" << endl;
        printSyntaxTree(node.children[0], level + 1);
        if (!node.value.empty()) {
            for (int i = 0; i <= level; ++i) cout << "    ";
            cout << node.value << endl;
            printSyntaxTree(node.children[1], level + 1);
        }
        break;
    case NodeType::RELATION:
        cout << "<Relation>: " << node.value << endl;
        break;
    case NodeType::CONDITION:
        cout << "<Condition>" << endl;
        printSyntaxTree(node.children[0], level + 1);
        for (int i = 0; i <= level; ++i) cout << "    ";
        cout << node.value << endl;
        printSyntaxTree(node.children[1], level + 1);
        break;
    case NodeType::PATTERN:
        cout << "<Pattern>: " << node.value << endl;
        break;
    default:
        break;
    }
}

// 递归下降解析器函数声明
Node parseQuery(string sql);
Node parseSelList(string selList);
Node parseFromList(string fromList);
Node parseCondition(string condition);

int main() {
    string sql = "SELECT name1, name2 "
                 "FROM r1, r2 "
                 "WHERE attr1 >= num1 AND attr2 IN ("
                     "SELECT name_in "
                     "FROM r_in "
                     "WHERE attr_in LIKE '%1960'"
                 ")";
    cout << "SQL 语句: \n" << sql << endl;
    cout << endl;

    // 解析SQL语句并构建语法树
    Node queryNode = parseQuery(sql);

    // 打印语法树
    cout << "语法树: " << endl;
    printSyntaxTree(queryNode);

    return 0;
}

Node parseQuery(string sql) {
    // 创建一个 Query 节点
    Node queryNode;
    queryNode.type = NodeType::QUERY;

    // 找到 SELECT 关键字的位置
    size_t posSelect = sql.find("SELECT");
    if (posSelect == string::npos) {
        cerr << "错误：缺少 SELECT 关键字" << endl;
        return queryNode;
    }

    // 找到 FROM 关键字的位置
    size_t posFrom = sql.find("FROM");
    if (posFrom == string::npos) {
        cerr << "错误：缺少 FROM 关键字" << endl;
        return queryNode;
    }

    // 找到 WHERE 关键字的位置
    size_t posWhere = sql.find("WHERE");
    if (posWhere == string::npos) {
        cerr << "错误：缺少 WHERE 关键字" << endl;
        return queryNode;
    }

    // 解析 SELECT 子句
    string selectClause = sql.substr(posSelect + 6, posFrom - posSelect - 6);
    queryNode.children.push_back(parseSelList(selectClause));

    // 解析 FROM 子句
    string fromClause = sql.substr(posFrom + 4, posWhere - posFrom - 4);
    queryNode.children.push_back(parseFromList(fromClause));

    // 解析 WHERE 子句
    string whereClause = sql.substr(posWhere + 5);
    queryNode.children.push_back(parseCondition(whereClause));

    return queryNode;
}

Node parseSelList(string selList) {
    // 创建一个 SelList 节点
    Node selListNode;
    selListNode.type = NodeType::SEL_LIST;

    // 查找逗号的位置
    size_t posComma = selList.find(",");
    if (posComma != string::npos) {
        // 如果找到逗号，则将当前节点的值设为 ","
        selListNode.value = ",";

        // 创建逗号左边的关系名称节点，类型为ATTRIBUTE
        string leftAttribute = selList.substr(0, posComma);
        // 去除前导和尾随空格
        leftAttribute.erase(0, leftAttribute.find_first_not_of(" "));
        leftAttribute.erase(leftAttribute.find_last_not_of(" ") + 1);
        Node leftAttributeNode;
        leftAttributeNode.type = NodeType::ATTRIBUTE;
        leftAttributeNode.value = leftAttribute;
        selListNode.children.push_back(leftAttributeNode);

        // 创建逗号右边的子节点，暂不确定类型，并递归解析
        string rightSelList = selList.substr(posComma + 1); 
        Node rightSelListNode = parseSelList(rightSelList);
        selListNode.children.push_back(rightSelListNode);
    }
    else {
        // 如果没有逗号，则直接创建一个节点，类型为ATTRIBUTE
        // 去除前导和尾随空格
        selList.erase(0, selList.find_first_not_of(" "));
        selList.erase(selList.find_last_not_of(" ") + 1);
        Node attributeNode;
        attributeNode.type = NodeType::ATTRIBUTE;
        attributeNode.value = selList;
        selListNode.children.push_back(attributeNode);
    }

    return selListNode;
}

Node parseFromList(string fromList) {
    // 创建一个 FromList 节点
    Node fromListNode;
    fromListNode.type = NodeType::FROM_LIST;

    // 查找逗号的位置
    size_t posComma = fromList.find(",");
    if (posComma != string::npos) {
        // 如果找到逗号，则将当前节点的值设为 ","
        fromListNode.value = ",";

        // 创建逗号左边的关系名称节点，类型为RELATION
        string leftRelation = fromList.substr(0, posComma);
        // 去除前导和尾随空格
        leftRelation.erase(0, leftRelation.find_first_not_of(" "));
        leftRelation.erase(leftRelation.find_last_not_of(" ") + 1);
        Node leftRelationNode;
        leftRelationNode.type = NodeType::RELATION;
        leftRelationNode.value = leftRelation;
        fromListNode.children.push_back(leftRelationNode);

        // 创建逗号右边的子节点，暂不确定类型，递归解析
        string rightFromList = fromList.substr(posComma + 1);
        Node rightFromListNode = parseFromList(rightFromList);
        fromListNode.children.push_back(rightFromListNode);
    }
    else {
        // 如果没有逗号，则直接创建一个节点，类型为RELATION
        // 去除前导和尾随空格
        fromList.erase(0, fromList.find_first_not_of(" "));
        fromList.erase(fromList.find_last_not_of(" ") + 1);
        Node relationNode;
        relationNode.type = NodeType::RELATION;
        relationNode.value = fromList;
        fromListNode.children.push_back(relationNode);
    }

    return fromListNode;
}

Node parseComparison(const string& condition, const string& symbol) {
    Node conditionNode;

    size_t posEqual = condition.find(symbol);
    if (posEqual != string::npos) {
        conditionNode.type = NodeType::CONDITION;
        // 解析属性比较
        string leftAttribute = condition.substr(0, posEqual);
        string rightAttribute = condition.substr(posEqual + symbol.length());
        conditionNode.value = symbol;
        // 解析左右属性，并作为子节点添加到 Condition 节点中
        Node leftAttributeNode;
        leftAttributeNode.type = NodeType::ATTRIBUTE;
        leftAttributeNode.value = leftAttribute;
        conditionNode.children.push_back(leftAttributeNode);
        Node rightAttributeNode;
        rightAttributeNode.type = NodeType::ATTRIBUTE;
        rightAttributeNode.value = rightAttribute;
        conditionNode.children.push_back(rightAttributeNode);
        return conditionNode;
    }

    return conditionNode;
}

Node parseCondition(string condition) {
    // 创建一个 Condition 节点
    Node conditionNode;
    conditionNode.type = NodeType::CONDITION;

    // 去除空格
    //condition.erase(remove_if(condition.begin(), condition.end(), ::isspace), condition.end());

    // 解析 AND 运算
    size_t posAnd = condition.find("AND");
    if (posAnd != string::npos) {
        string leftCondition = condition.substr(0, posAnd);
        string rightCondition = condition.substr(posAnd + 3); // 跳过 "AND"
        conditionNode.value = "AND";
        conditionNode.children.push_back(parseCondition(leftCondition));
        conditionNode.children.push_back(parseCondition(rightCondition));
        return conditionNode;
    }

    // 解析 IN 子查询
    size_t posIn = condition.find("IN");
    if (posIn != string::npos) {
        string attributeName = condition.substr(0, posIn);
        size_t posLeftParenthesis = condition.find("(", posIn);
        size_t posRightParenthesis = condition.find(")", posLeftParenthesis);
        string subQuery = condition.substr(posLeftParenthesis + 1, posRightParenthesis - posLeftParenthesis - 1);
        conditionNode.value = "IN";
        // 解析属性，并作为子节点添加到 Condition 节点中
        Node attributeNode;
        attributeNode.type = NodeType::ATTRIBUTE;
        attributeNode.value = attributeName;
        conditionNode.children.push_back(attributeNode);
        // 解析子查询，并作为子节点添加到 Condition 节点中
        conditionNode.children.push_back(parseQuery(subQuery));
        return conditionNode;
    }

    Node comparisonNode;

    // 解析比较符号
    const vector<string> comparisonSymbols = { "<=", ">=", "=", "<", ">" };
    for (const auto& symbol : comparisonSymbols) {
        comparisonNode = parseComparison(condition, symbol);
        if (comparisonNode.type == NodeType::CONDITION) {
            return comparisonNode;
        }
    }

    // 解析 LIKE 子查询
    size_t posLike = condition.find("LIKE");
    if (posLike != string::npos) {
        string attributeName = condition.substr(0, posLike);
        string pattern = condition.substr(posLike + 4); // 跳过 "LIKE"
        conditionNode.value = "LIKE";
        // 解析属性和模式，并作为子节点添加到 Condition 节点中
        Node attributeNode;
        attributeNode.type = NodeType::ATTRIBUTE;
        attributeNode.value = attributeName;
        conditionNode.children.push_back(attributeNode);
        Node patternNode;
        patternNode.type = NodeType::PATTERN;
        patternNode.value = pattern;
        conditionNode.children.push_back(patternNode);
        return conditionNode;
    }

    // 如果条件不符合以上任何一种形式，则错误
    cerr << "Error: Invalid condition." << endl;
    return conditionNode;
}

控制台输出

SQL 语句:
SELECT name1, name2 FROM r1, r2 WHERE attr1 >= num1 AND attr2 IN (SELECT name_in FROM r_in WHERE attr_in LIKE '%1960')

语法树:
<Query>
    SELECT
    <SelList>
        <Attribute>: name1
        ,
        <SelList>
            <Attribute>: name2
    FROM
    <FromList>
        <Relation>: r1
        ,
        <FromList>
            <Relation>: r2
    WHERE
    <Condition>
        <Condition>
            <Attribute>:  attr1
            >=
            <Attribute>:  num1
        AND
        <Condition>
            <Attribute>:  attr2
            IN
            (
            <Query>
                SELECT
                <SelList>
                    <Attribute>: name_in
                FROM
                <FromList>
                    <Relation>: r_in
                WHERE
                <Condition>
                    <Attribute>:  attr_in
                    LIKE
                    <Pattern>:  '%1960'
            )

实验四：事务调度管理实验

一、实验题目

实验目标

通过该任务，掌握事务调度原理，特别是基于时间戳的调度以及调度过程中时间戳的变化等。

实验要求

1. 编程语言不限，只要实现功能流程即可，不限制界面要求等；
2. 初始化一个事务列表的时间戳，给定各事务操作列表及执行顺序，输出在公共资源上各时间戳变化等，可以以课本7.26为例；

二、实现

实现了一种简单的基于时间戳的调度规则（有Thomas写规则）。

1. 分析

定义

• RT(x): 最后读x的事务的时间戳
• WT(x): 最后写x的事务的时间戳
• TS(T): 事务T启动时的时间戳

调度规则

• 读操作：若事务 T 读数据 x
  • 若T事务读x，则将T的时间戳TS与WT(x)比较
    • 若TS大(T后进行)，则允许T操作，并且更改RT(x)为max{RT(x),TS}
    • 否则，有冲突，撤回T，重启T（读-写冲突）
• 写操作：若事务 T 写数据 x
  • 将T的时间戳TS与RT(x)比较
    • 若TS大(T后进行)，则允许T操作，并且更改WT(x)为max{WT(x),TS}
    • 否则，有冲突，撤回T重做（写-读冲突）
  • 将T的时间戳TS与WT(x)比较
    • 若TS大，则允许T写，并且更改WT(x)为T的时间戳；
    • 否则，T写入的值是过时的，可以忽略写操作，事务T继续执行（Thomas写规则）

2. 实验结果

代码和详细注释

#include <iostream>
#include <vector>
#include <map>
#include <algorithm>
#include <queue>
using namespace std;

struct Execution {
    int id;     // 事务编号
    char op;    // 进行的操作
    char res;   // 该操作使用的资源
};

queue<Execution> executionList;
// wt(Q) 表示成功执行 write(Q) 的所有事务中最大的时间戳，rt(Q) 表示成功执行 read(Q) 的所有事务中最大的时间戳。
map<char, int> rt, wt;
bool state[4];  // 标识事务是否回滚
int ts[] = { 0, 200, 150, 175 };  // 初始化事务时间戳，事务从下标 1 开始

// 模拟调度并输出时间戳变化
void simulateScheduling() {
    cout << endl;
    cout << "\t\tT1\t" << "\tT2\t" << "\tT3\t" << endl;
    cout << "进入时间戳\t" << ts[1] << "\t\t" << ts[2] << "\t\t" << ts[3] << endl;
    cout << endl;
    for (int step = 1; executionList.size(); step++) {
        Execution execution = executionList.front();
        executionList.pop();
        int id = execution.id;
        char op = execution.op;
        char res = execution.res;
        // 回滚的事务不执行
        if (state[id]) {
            continue;
        }

        cout << "第 " << step << " 步，事务 " << id << " 执行操作 " << op << '(' << res << ')';
        
        if (op == 'R') {
            if (ts[id] > wt[res]) {
                rt[res] = max(rt[res], ts[id]);
                cout << " 成功，RT(" << res << ") = " << rt[res] << endl;
            }
            else {
                cout << " 失败，事务回滚。" << endl;
                state[id] = true;
            }
        }
        else {
            if (ts[id] < rt[res]) {
                cout << " 失败，事务回滚。" << endl;
                state[id] = true;
            }
            else if (ts[id] < wt[res]) {
                cout << " 失败，过时的写，不进行写入。" << endl;
            }
            else if (ts[id] > rt[res]) {
                wt[res] = max(wt[res], ts[id]);
                cout << " 成功，WT(" << res << ") = " << wt[res] << endl;
            }
            else if (ts[id] > wt[res]) {
                wt[res] = ts[id];
                cout << " 成功，WT(" << res << ") = " << wt[res] << endl;
            }
        }
        cout << endl;
    }
}

int main() {
    // 测试用例，按时间戳进行这些操作 {事务编号, 读/写, 操作的资源}
    executionList.push({ 1, 'R', 'B' });
    executionList.push({ 2, 'R', 'A' });
    executionList.push({ 3, 'R', 'C' });
    executionList.push({ 1, 'W', 'B' });
    executionList.push({ 1, 'W', 'A' });
    executionList.push({ 2, 'W', 'C' });
    executionList.push({ 3, 'W', 'A' });

    simulateScheduling();

    return 0;
}

控制台输出

                T1              T2              T3
进入时间戳      200             150             175

第 1 步，事务 1 执行操作 R(B) 成功，RT(B) = 200

第 2 步，事务 2 执行操作 R(A) 成功，RT(A) = 150

第 3 步，事务 3 执行操作 R(C) 成功，RT(C) = 175

第 4 步，事务 1 执行操作 W(B) 成功，WT(B) = 200

第 5 步，事务 1 执行操作 W(A) 成功，WT(A) = 200

第 6 步，事务 2 执行操作 W(C) 失败，事务回滚。

第 7 步，事务 3 执行操作 W(A) 失败，过时的写，不进行写入。

实验五：关联规则挖掘算法实验

一、实验题目

实验目标

通过该任务，掌握关联规则挖掘算法，了解数据挖掘基本过程。

实验要求

1. 编程语言不限，只要实现功能流程即可，不限制界面要求等；
2. 实现Apriori算法即可，如果有余力，可以实现各种改进版本的Apriori算法；
3. 输入：构造一些项集，输入特定支持度、置信度等参数，输出相应的频繁项集。

二、实现

1. 分析

算法流程

1. 输入数据集 dataSet
2. 确定数据集 dataSet 中所包含的项集，不重复
3. 进行第一次迭代，把每个项集中的项目单独扫描统计（即某个项在多少个交易记录中出现了），将每个项都作为候选 1 项集 C1 的成员，并计算每个项的支持度
4. 根据候选项集 C1 的成员，比较其支持度和最小支持度，大于等于最小支持度的为候选项集 C2
5. 保持最小支持度不变，重复进行第四步，直到没有满足最小支持度的项集，此时输出最终频繁项集
6. 根据 k 项集 Ck 和 k+1 项集 Ck+1，计算 k 项集的置信度，满足最小置信度的则筛选存储
7. 重复第六步，k 值从 1 开始，直到到最大值，返回具有强相关的关联规则列表

2. 实验结果

代码和详细注释

# 构建候选项集 C1
# 扫描所有的订单，获取所有商品的集合
def createC1(dataSet):
    items = []
    for basket in dataSet:
        for item in basket:
            items.append(item)
    
    # 使用 set() 函数去除重复项，并转换为列表形式
    unique_items = list(set(items))
    # 对列表进行排序
    unique_items.sort()

    # 将每个项放入一个列表中，形成二维列表
    Ck = [[x] for x in unique_items]
    Ck = list(map(frozenset, Ck))
    
    return Ck


# 根据最小支持度，从候选项集Ck里筛选出符合最小支持度的频繁项集Lk
# dataset：原始数据集
# Ck: 候选集
# minSupport: 支持度的最小值
def makeLk(dataset, Ck, minSupport):
    # 初始化候选集计数字典
    candidate_counts = {}
    for transaction in dataset:
        for candidate in Ck:
            if candidate.issubset(transaction):
                if candidate not in candidate_counts:
                    candidate_counts[candidate] = 1
                else:
                    candidate_counts[candidate] += 1

    num_items = float(len(dataset))
    Lk = []
    support_data = {}       # 用于存储支持度信息

    # 遍历候选项集，计算支持度并判断是否满足最小支持度要求
    for candidate in candidate_counts:
        support = candidate_counts[candidate] / num_items
        if support >= minSupport:
            Lk.append(candidate)
        support_data[candidate] = support

    return Lk, support_data


# 将频繁项集 L[k-1] 通过拼接得到候选 Ck 项集将频繁项集Lk-1，以便 makeLk 函数用来生成频繁项集 Lk
def generateCk(Lk_1, k):
    Ck = []
    lenLk = len(Lk_1)
    for i in range(lenLk):
        L1_list = list(Lk_1[i])
        L1 = L1_list[:k - 2]
        L1.sort()
        for j in range(i + 1, lenLk):
            L2_list = list(Lk_1[j])
            L2 = list(Lk_1[j])[:k - 2]
            L2.sort()
            # 如果前 k-2 个项相同，则合并两个集合
            if L1 == L2:
                Ck.append(Lk_1[i] | Lk_1[j])
    return Ck


# 获取并保存每一级的的频繁项集 L，以便之后计算指定频繁项的置信度
def apriori(dataSet, minSupport=0.5):
    C1 = createC1(dataSet)
    L1, supportData = makeLk(dataSet, C1, minSupport)
    L = [L1]

    # 输出第一级频繁项集
    print("======================================================")
    print("频繁项集第 1 级:")
    for item in L1:
        print(f"{set(item)} 支持度: {supportData[item]}")

    k = 2
    while len(L[k - 2]) > 0:
        print("======================================================")
        Lk_1 = L[k - 2]
        Ck = generateCk(Lk_1, k)
        Lk, supK = makeLk(dataSet, Ck, minSupport)
        if len(Lk) == 0:
            break

        print("频繁项集第 {} 级:".format(k))
        for item in Lk:
            print(f"{set(item)} 支持度: {supK[item]}")
        
        supportData.update(supK)
        L.append(Lk)
        k += 1
    return L, supportData


# 根据频繁项集 L 和最小置信度生成强关联规则
# L: 频繁项集列表
# supportData: 包含频繁项集支持数据的字典
# minConf 最小置信度
def generateRules(L, supportData, minConf=0.7):
    # 存储生成的关联规则的列表
    rules = []
    # 遍历频繁项集列表
    for i in range(1, len(L)):
        for freqSet in L[i]:
            # 生成单个项的关联规则
            H1 = [frozenset([item]) for item in freqSet]
            if i > 1:
                # 对于长度大于1的频繁项集，递归生成关联规则
                rules_from_conseq(freqSet, H1, supportData, rules, minConf)
            else:
                # 对于长度为1的频繁项集，直接计算关联规则
                calc_conf(freqSet, H1, supportData, rules, minConf)
    return rules


# 用来进行剪枝操作，计算是否满足最小置信度
def calc_conf(freqSet, H, supportData, rules, minConf=0.7):
    # 存储修剪后的后件列表
    prunedH = []
    # 遍历每个候选关联规则
    for conseq in H:
        # 计算置信度
        P_A = supportData[freqSet.difference(conseq)]
        conf = supportData[freqSet] / P_A
        # 如果置信度满足最小置信度要求，则加入关联规则列表
        if conf >= minConf:
            print(f"{set(freqSet - conseq)} --> {set(conseq)} 置信度: {conf}")
            rules.append((freqSet - conseq, conseq, conf))
            prunedH.append(conseq)
    return prunedH


# 用来获取所有满足最小置信度的强关联规则
def rules_from_conseq(freqSet, H, supportData, rules, minConf=0.5):
    # 后件长度
    m = len(H[0])
    # 如果频繁项集的长度大于后件长度加1
    if len(freqSet) > (m + 1):
        # 生成下一级候选后件集
        Hmp1 = generateCk(H, m + 1)
        # 计算新的关联规则
        Hmp1 = calc_conf(freqSet, Hmp1, supportData, rules, minConf)
        # 如果新的关联规则不为空，则继续递归生成
        if len(Hmp1) > 0:
            rules_from_conseq(freqSet, Hmp1, supportData, rules, minConf)


# 书上的例子
dataset = [
        ['BI', 'BS', 'BU'],
        ['HP1', 'HP2', 'HP3'],
        ['BI', 'HP1'],
        ['BI', 'BS', 'HP1', 'HP2'],
        ['BI', 'BS', 'BU', 'HP1'],
        ['BI', 'BU'],
        ['BS', 'HP1', 'HP2'],
        ['BI', 'BS', 'HP1', 'HP2', 'HP3']
    ]

print("======================================================")
minSupport = 0.5    # 最小支持度，0.5 表示在 8 个集合中至少出现 4 次，相当于书本中的 s=4
minConf = 0       # 最小置信度
print(f"最小支持度 = {minSupport}   最小置信度 = {minConf}")

L, supportData = apriori(dataset, minSupport)

rules = generateRules(L, supportData, minConf)

print("======================================================")

控制台输出

======================================================
最小支持度 = 0.5   最小置信度 = 0
======================================================
频繁项集第 1 级:
{'BI'} 支持度: 0.75
{'BS'} 支持度: 0.625
{'HP1'} 支持度: 0.75
{'HP2'} 支持度: 0.5
======================================================
频繁项集第 2 级:
{'BS', 'BI'} 支持度: 0.5
{'HP2', 'HP1'} 支持度: 0.5
{'HP1', 'BI'} 支持度: 0.5
{'HP1', 'BS'} 支持度: 0.5
======================================================
{'BI'} --> {'BS'} 置信度: 0.6666666666666666
{'BS'} --> {'BI'} 置信度: 0.8
{'HP1'} --> {'HP2'} 置信度: 0.6666666666666666
{'HP2'} --> {'HP1'} 置信度: 1.0
{'BI'} --> {'HP1'} 置信度: 0.6666666666666666
{'HP1'} --> {'BI'} 置信度: 0.6666666666666666
{'BS'} --> {'HP1'} 置信度: 0.8
{'HP1'} --> {'BS'} 置信度: 0.6666666666666666
======================================================