常见排序算法总结
插入排序
1. 直接插入排序
基本思想
在待排序序列中,每趟排序从前往后找,一旦发现逆序元素,就将其插入到前面已排好序的序列中的合适位置。
性质
- 稳定
- 每趟排序可能不会将元素被放到最终位置
- 时间复杂度:O(n^2);总比较次数与总移动次数均约为n^2/4
- 基本思想:每轮排序中选择未排序序列中的第一个元素,将其插入到前面已排序序列的合适位置。
实现
void InsertSort(int a[], int n) {
for (int i=1; i<n; i++) {
if (a[i]<a[i-1]) {
int k=a[i];
for (int j=i-1; k<a[j] && j>=0; j--)
a[j+1]=a[j];
a[j+1]=k;
}
}
}
2. 折半插入排序
基本思想
先折半查找出元素的待插入位置,然后统一移动待插入位置之后的所有元素。
性质
- 稳定
- 仅适用于顺序存储的线性表
- 基本思想:先折半查找出元素的待插入位置,然后统一移动待插入位置之后的所有元素。
- ⚠️注意:在这里,h+1 最后一定指向比 k 大的第一个数!即 a[h] <= k , a[h+1] > k
实现
void InsertSort(int a[], int n) {
for (int i=1; i<n; i++) {
int k=a[i], l=0, h=i-1;
while (l<=r) {
int mid=(l+h)<<1;
if (k<a[mid]) h=mid-1;
else l=mid+1;
}
// 此时h+1最后一定指向比k大的第一个数!即 a[h]<=k, a[h+1]>k
for (int j=i-1; j>=h+1; j--)
a[j+1]=a[j];
a[h+1]=k;
}
}
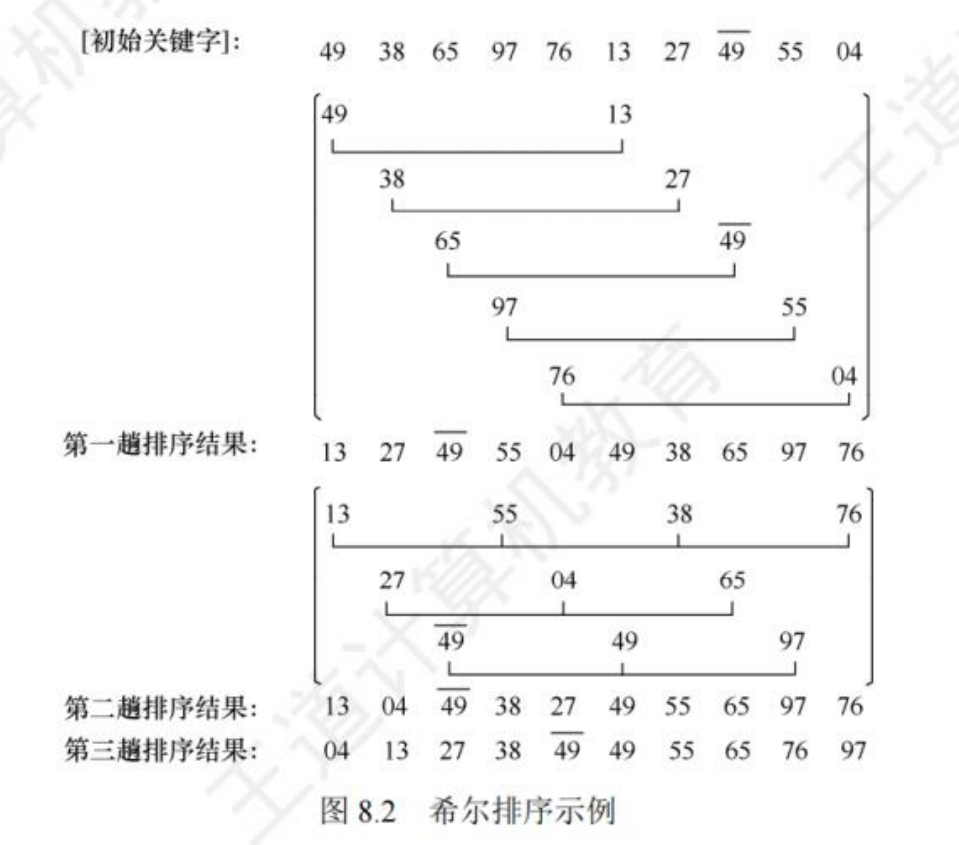
3. 希尔排序(缩小增量排序)
基本思想
根据一个特定增量,将待排序表分割为若干子表,对每个子表分别进行直接插入排序。
性质
- 稳定
- 适用于基本有序或者数据量不大的排序表
- 时间复杂度:O(n^2);n在某个特定范围时,时间复杂度约为O(n^1.3)
实现
void ShellSort(int a[], int n) {
for (int dk=n/2; dk>=1; dk/=2) {
for (int i=dk; i<n; i++) {
if (a[i]<a[i-dk]) {
int k=a[i];
for (int j=i-dk; j>=0 && k<a[j]; j-=dk)
a[j+dk]=a[j];
a[j+dk]=k;
}
}
}
}
交换排序
1. 冒泡排序
基本思想
(此处只讲最小元素上浮的思路)在待排序序列中,每趟排序从后往前两两比较相邻元素的值,若为逆序,则交换它们,直到比较到待排序序列的第一个位置,这个位置的元素加入到前面已排好序的序列中。然后继续处理长度减一后的待排序序列。每次都会将待排序序列的最小元素上浮到前面。
性质
- 稳定
- 适用于顺序存储和链式存储的线性表
- 每趟排序都会有一个元素被放到最终位置
- 时间复杂度:最好O(n),最坏O(n^2),平均O(n^2)
- 空间复杂度:O(1)
- 每次比较需要移动元素3次来交换位置
- 最多 n-1 趟可以排好,此时比较次数为 n(n-1)/2,移动次数为 3n(n-1)/2
实现
void BubbleSort(int a[], int n) {
bool flag=false;
for (int i=0; i<n; i++) {
for (int j=n-1; j>i; j--) {
if (a[j]<a[j-1]) {
swap(a[j], a[j-1]);
flag=true;
}
}
if (!flag) return;
}
}
2. 快速排序
基本思想
基于分治法:每趟排序选取一个枢轴,排序后枢轴左边的元素都小于枢轴,右边的元素都大于枢轴。每趟排序并不会产生有序子序列,但会使枢轴元素放在其最终位置上。
性质
- 不稳定
- 仅适用于顺序存储的线性表
- 每趟排序都会有一个元素(枢轴)被放到最终位置
- 时间复杂度:最坏O(n^2)(基本有序或逆序时),平均(nlogn)
- 是所有内部排序算法中平均性能最优的排序算法
- 需要借助递归工作栈
- 容量与递归调用的最大层数一致
- 最坏情况下,要进行n-1次递归调用,栈的深度为O(n)
- 平均情况下,栈的深度为O(logn)
实现
void QuickSort(int a[], int low, int high) {
if (low>=high) return;
int i=low, j=high, pivot=a[low];
while (low<high) {
while (low<high && a[j]>=pivot) j--;
a[i]=a[j];
while (low<high && a[i]<=pivot) i++;
a[j]=a[i];
}
a[i]=pivot;
QuickSort(a, low, i-1);
QuickSort(a, i+1, high);
}
选择排序
1. 简单选择排序
基本思想
每一趟(第 i 趟)在后面的 n-i+1 个待排序元素中选出关键字最小的元素,作为前面有序子序列的第 i 个元素。
性质
- 不稳定
- 适用于顺序存储和链式存储的线性表,以及关键字较少的情况
- 时间复杂度:O(n^2);空间复杂度:O(1)
- 元素的比较次数与序列的初始状态无关,始终是 n(n-1)/2 次
实现
void SelectSort(int a[], int n) {
for (int i=0; i<n-1; i++) {
int min=i;
for (int j=i+1; j<n; j++)
if (a[j]<a[min]) min=j;
if (min!=i) swap(a[i], a[min]);
}
}
2. 堆排序
基本思想(大根堆为例)
大根堆:升序。小根堆:降序。
- 将待排序序列构造成一个大根堆
- 此时整个序列的最大值就是堆的根节点
- 将其与末尾元素进行交换,此时末尾就为最大值,此时末尾处于有序子序列中。
- 然后将剩余的前 n-1 个待排序元素重新构造成一个堆,这样会得到这 n-1 个元素中的最大值,将其与这 n-1 个元素的末尾元素交换。如此反复执行(n-2, n-3, ...),便能得到一个有序序列了。
性质
- 不稳定
- 建堆时间为O(n),每次调整的时间复杂度为O(logn)(即堆的高度),所有情况下时间复杂度都为O(nlogn);空间复杂度为O(1)
- 仅适用于顺序存储的线性表
实现
// 调整大根堆(对以元素k为根的子树进行调整)
void HeapAdjust(int a[], int k, int len) {
int tmp=a[k];
for (int i=k*2+1; i<len; i=i*2+1) {
if (i+1<len && a[i+1]>a[i]) i++;
if (tmp<a[i]) {
a[k]=a[i]; // 将较小的子结点赋给根节点,此时根节点原值已经保存,不急着给子结点
k=i; // 下一轮对根为i的子树进行调整
}
else break;
}
a[k]=tmp; // 最后将原根节点赋给最后的子结点
}
// 堆排序
void HeapSort(int a[], int len) {
// 建堆,从最后一个非叶结点开始向前调整
for (int i=n/2-1; i>=0; i--)
HeapAdjust(a, i, len);
for (int i=len-1; i>0; i--) {
swap(a[0], a[j]); // 输出堆顶元素(和堆底元素交换)
HeapAdjust(a, 0, i-1); // 调整剩余的 i-1 个元素成堆
}
}
归并排序、基数排序
1. 归并排序
基本思想
基于分治,将两个或两个以上的有序表合并成一个新的有序表。
性质
- 稳定
- 时间复杂度:O(nlogn)。每趟归并的时间复杂度为O(n),共需进行 ⌈logn⌉ 趟归并
- 空间复杂度:O(n)。Merge()操作需要使用辅助空间
- 适用于顺序存储和链式存储的线性表
实现
int b[N]; // 辅助数组
void MergeSort(int a[], int l, int h) {
if (l>=h) return;
int mid=l+r>>1;
MergeSort(a, l, mid);
MergeSort(a, mid+1, h);
int i=l, j=mid+1, k=0;
while (i<=mid && j<=h) {
if (a[i]<a[j]) b[k++]=a[i++];
else b[k++]=a[j++];
}
while (i<=mid) b[k++]=a[i++];
while (j<=h) b[k++]=a[j++];
for (int i=l, j=0; i<=h; i++,j++) a[i]=b[j];
}
2. 基数排序
基本思想
基于关键字各位的大小进行排序。处理从小到大的各个数字位,被称作“最低位优先”(LSD)方法;或者,处理从大到小的各个数字位,称为“最高位优先”(MSD)方法。
性质
-
稳定
-
不基于比较和移动进行排序
-
时间复杂度:O(d(n+r))。与序列的初始状态无关
-
空间复杂度:O(r)
d:分配和收集操作的趟数。n:关键字个数。r:进制数/队列数
实现
代码实现略,此处为动图演示。

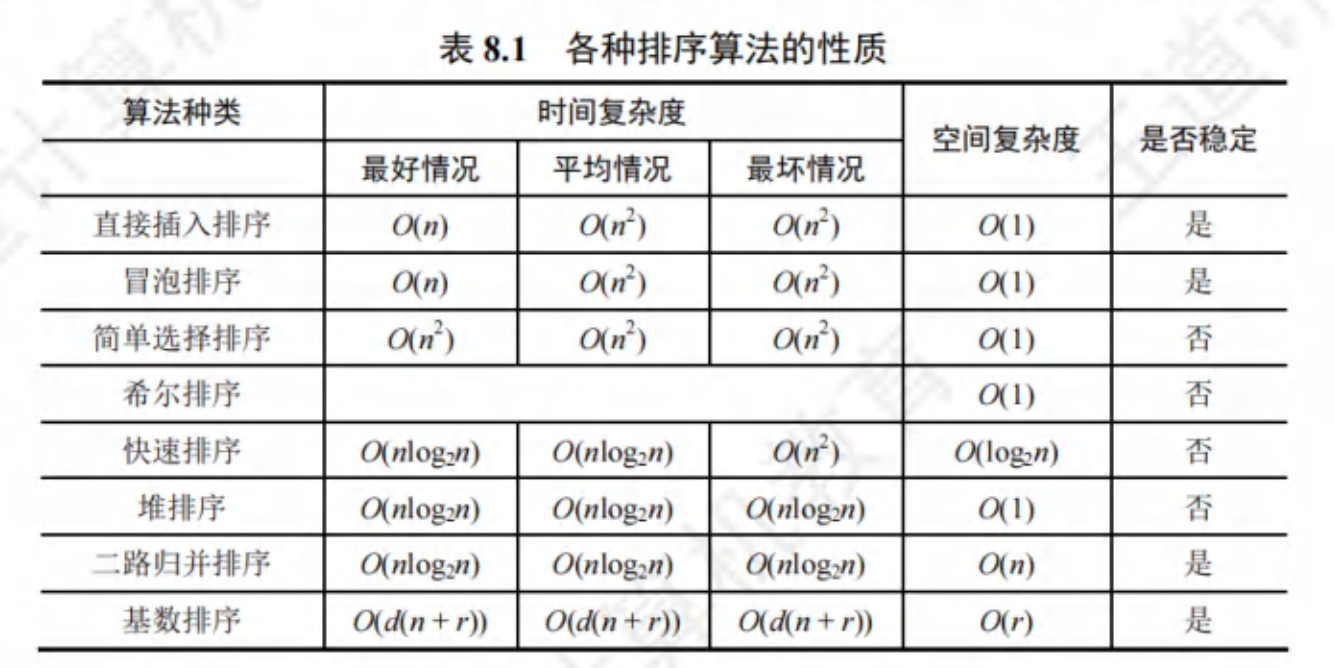
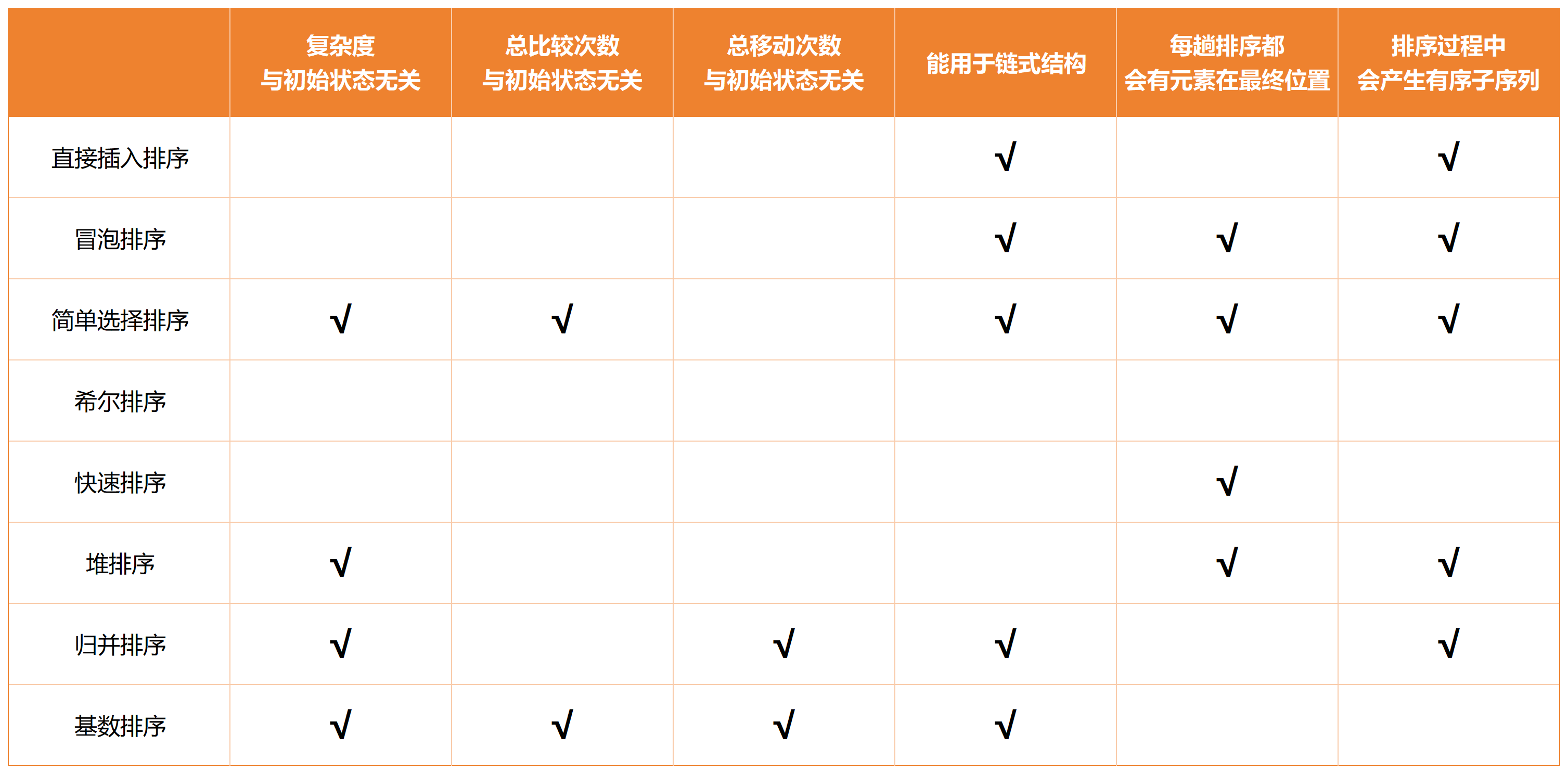
各种排序算法比较