5x5一字棋 博弈树搜索 原理/C++代码完整实现/详细注释

实验要求

实践博弈树搜索——“5x5格子的一字棋问题”。要求是Max方和Min方都用博弈树来决策，或者一方使用博弈树决策，一方随机或手工走棋，并使用alpha和beta减枝。

理论知识

与/或树的启发式搜索策略

基本概念

• 与/或树用于分解复杂问题，表示问题求解的递归结构。

  • 与节点表示必须解决所有子问题才能解决当前问题。
  • 或节点表示只需解决其中一个子问题即可解决当前问题。

• 解树：与/或树中的解是由可解节点构成的子树，包含起始节点到所有子问题的路径。

搜索过程

• 启发式搜索利用估价函数对与/或树节点的代价进行估算，形成“希望树”，即从初始节点到终点的最优解路径。
• 搜索过程中，算法通过不断标记节点（可解或不可解）来确认解树，最终找到解树或确定问题无解。

博弈树的启发式搜索策略

基本概念

博弈树是一种用于描述二人对弈过程的树结构，符合“与/或树”的规则，但层次交替出现，MAX节点和MIN节点轮流行动。

• 或节点（MAX节点，位于奇数层）：代表当前行动方希望选择收益最大的路径。
• 与节点（MIN节点，位于偶数层）：对方希望选择让当前行动方最小化收益的路径。
• 在博弈树中，“或”节点和“与”节点是逐层交替出现的。自己一方扩展的节点之间是“或”关系，对方扩展的节点之间是“与”关系。双方轮流地扩展节点。

基本搜索策略

极小极大搜索（min-max）

优化的搜索方法：α-β剪枝法

• 剪枝
• 倒推估值与生成同时进行

为什么MAX方是或节点，MIN方是与节点？

• 如果我们站在MAX方的立场上，则可供MAX方选择的若干行动方案之间是“或”关系，因为主动权在MAX方手里，他或者选择这个行动方案，或者选择另一个行动方案，完全由MAX方自已决定
• 当MAX方选取任一方案走了一步后，MIN方也有若干个可供选择的行动方案，此时这些行动方案对MAX方来说它们之间则是“与”关系，因为这时主动权操在MIN方手里，这些可供选择的行动方案中的任何一个都可能被MIN方选中，MAX方必须应付每一种情况的发生。

极大极小分析法

定义

极大极小分析法通过评估博弈树的节点值，确定每一步的最优选择。

从叶节点开始，计算其得分并向上回溯，每个MIN节点选择最小值，MAX节点选择最大值，最终确定最优行动方案。

算法流程

1. 需要根据问题的特性信息定义一个估值函数

2. 根据估值函数，从下往上估算当前博弈树端节点的得分。此时估算出来的得分称为静态估值

3. 当端节点的静态估值计算出来后，再推算出父节点的得分（倒推值）

   • MAX层节点从子节点选择最大的值
   • MIN层节点从子节点选择最小的值

4. 将每层选择出的节点串联，该路径即为到达最优值所在节点路径

α-β剪枝算法

α-β剪枝通过限制搜索的范围提高效率。把生成和倒推估值结合起来进行，再根据一定的条件判定，有可能尽早修剪掉一些无用的分枝。

定义

与倒推值的计算方法相同，或大与小。

• 一个MAX节点的α值等于其后继节点当前最大的最终倒推值，即下界（⚠️这个下界限定了修剪范围，它指的是当前MAX节点的子结点中最大的估值，如果后续新扩展的子结点估值比这个下界小，就说明这个子节点的子树没用，可以被修剪）
• 一个MIN节点的β值等于其后继节点当前最小的最终倒推值，即上界（⚠️与上界定义相反）
• MAX节点的α值永不减少
• MIN节点的β值永不增加​

α-β 剪枝

• α剪枝：设MAX节点的下限为α，则其所有的MIN子节点中，其评估值的β上限 ≤ MAX节点的α，其以下部分的搜索都可以停止了，即对这部分节点进行了α剪枝。

  ⚠️因为父节点MAX的倒推值选的是子节点MIN中最大的估值，当前MIN节点最大估值是β，它小于等于α，且MIN节点的β值永不增加​，所以后续扩展不可能再大于α，而且比α小的不可能会再作为父节点的新倒推值，说明该MIN节点之后扩展的子节点的估值对父节点的倒推值已无任何影响了，可剪去这些子节点

• β剪枝：设MIN节点的上限为β，则其所有的MAX子节点中，其评估值的α下限 ≥ MIN节点的β，其以下部分的搜索都可以停止了，即对这部分节点进行了β剪枝。

  ⚠️因为父节点MIN的倒推值选的是子节点MAX中最小的估值，当前MAX节点最大估值是α，它大于等于β，且MAX节点的α值永不减少，所以后续扩展不可能再小于β，而且比β大的不可能会再作为父节点的新倒推值，说明该MIN节点之后扩展的子节点的估值对父节点的倒推值已无任何影响了，可剪去这些子节点

例子

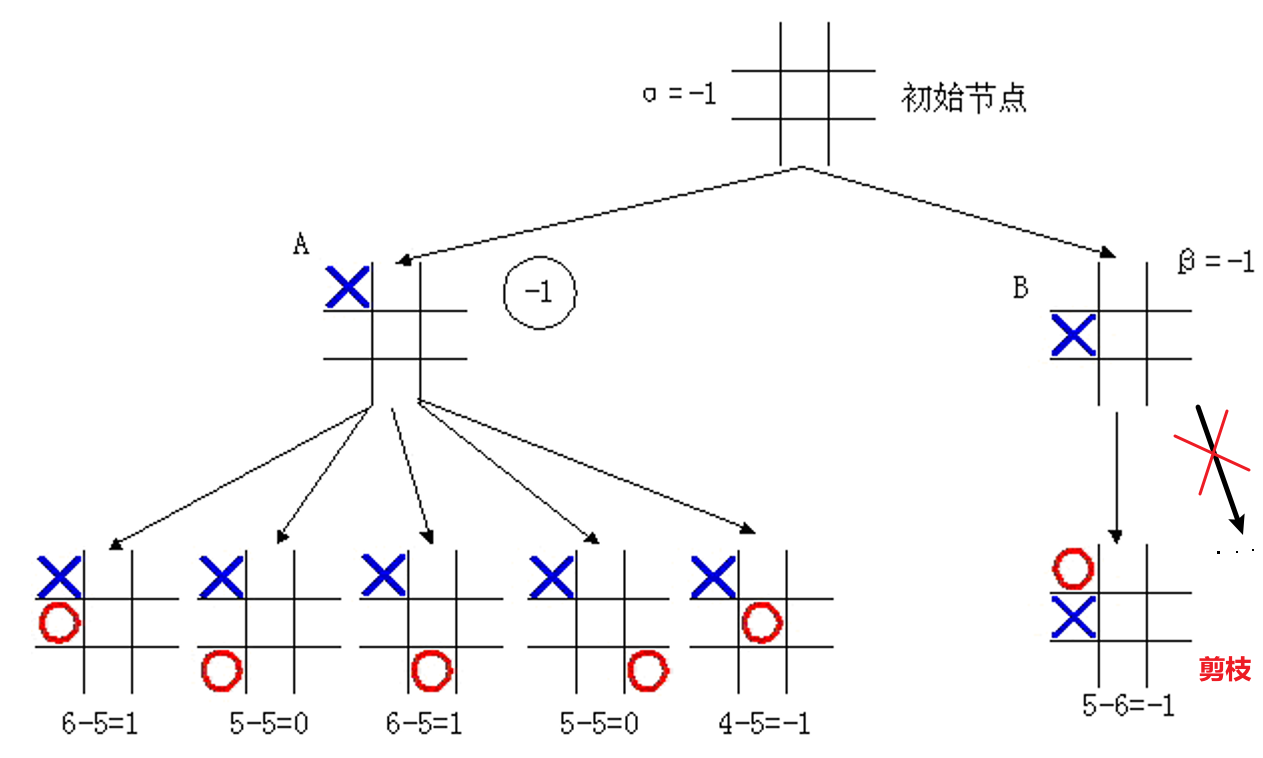
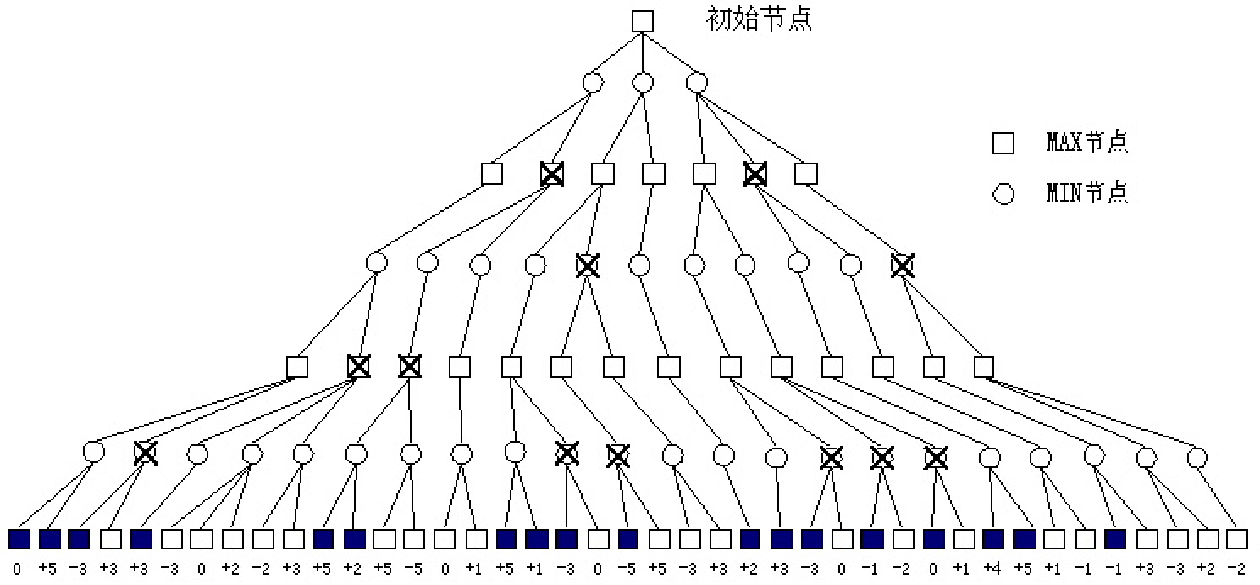
算法流程

博弈树搜索流程

1. 初始化棋盘

2. 检查是否有胜者，如果没有，执行下一步；如果有，输出结果

3. MAX/MIN方轮流下棋，对每一方的决策描述可以概括如下：

   1. 创建一个博弈树根节点，这个根节点为当前棋局（游戏刚开始时棋盘为空），第二层为当前出棋方所有可能的出棋情况

      1. 初始化所有节点的 α = -∞，β = +∞

   2. 进入minimax函数，开始构建博弈树

      1. 从根节点开始，递归调用minmax函数（至多调用depth层，其值由棋盘剩余空间动态改变）

         • 当前节点如果是非叶节点

           • 如果是MAX节点，则开始遍历其子节点：

             1. 对其中一个子节点调用minmax函数，传入自己的 α 和 β 值

             2. 获得返回值（即子节点的倒推值），利用返回值更新自身倒推值（MAX节点需要选取最大的值），以及自身的 α 值

                理论上MAX节点自身在任何时刻的倒推值都与其 α 值相等

             3. 剪枝：若自身的 α ≥ 父节点的 β，则停止遍历后续子节点，退出循环

                因为自身的 α 不可能再减小（MAX节点性质），然而自己当前的 α 值就已经不可能再影响父节点MIN的值更新，所以以这个MAX节点为根的子树都没用了

             4. 返回自身倒推值

           • 如果是MIN节点，则开始遍历其子节点：

             1. 对其中一个子节点调用minmax函数，传入自己的 α 和 β 值

             2. 获得返回值（即子节点的倒推值），利用返回值更新自身倒推值（MIN节点需要选取最小的值），以及自身的 β 值

                理论上MIN节点自身在任何时刻的倒推值都与其 β 值相等

             3. 剪枝：若自身的 β ≤ 父节点的 α，则停止遍历后续子节点，退出循环

                因为自身的 β 不可能再增大（MIN节点性质），然而自己当前的 β 值就已经不可能再影响父节点MAX的值更新，所以以这个MIN节点为根的子树都没用了

             4. 返回自身倒推值

         • 当前节点如果是叶子节点（棋盘已满/出现胜者/搜索已达最大深度）

           • 将评估函数应用于叶子节点，计算叶子节点的静态估值，并返回估值

             • 如果该节点是MAX获胜的节点，则将该节点估值设为无穷大

             • 如果该节点是MIN获胜的节点，则将该节点估值设为无穷小

               这里我把节点的无穷大/小的实际值分别设为了INT_MAX/2+depth和INT_MIN/2-depth，有以下两点原因：

               • 由于程序中 α 和 β 实际的初始值是INT_MIN和INT_MAX，所以节点估值的绝对值必须要比它们的绝对值小，否则该节点一定会引发剪枝行为
               • depth表示的是搜索的剩余深度，其值越大代表在博弈树中的深度越浅，如果有两个相同的致胜节点，那么深度浅的需要经过的回合是最少的，这种节点更容易获胜，它的depth值也越大，通过加减depth可以区分这些致胜节点的优先级

             • 如果都不是，则使用估值函数计算估值

               • 估值函数：e(P) = e(MAX可胜利的行、列或对角线的总数) - e(MIN可胜利的行、列或对角线的总数) + 棋盘位置权重

      2. minimax函数全部返回，此时根节点已选出子结点中最大/最小（看根节点是MAX还是MIN）的倒推值作为自己的倒推值

   3. 回到函数外，遍历所有子节点，找到倒推值与自身倒推值相同的子结点，就是最优选择（可能不止一个，但是只选择其中一个），下棋

4. 一方下完棋后，切换玩家，回到第 2 步

其他优化

• 为每个单元格赋予权重：处于对角线、靠近中心点的格子都会有更高的权重，它参与估值函数的计算。
• 剪枝时delete子节点，释放内存空间。
• 生成子节点时考虑棋盘对称性：对称棋盘的节点决策都是等效的，所以使用检测对称的函数来避免有对称棋盘的生成，降低决策步骤。
• 生成子节点时，通过打乱对空白格子的占有顺序，来打乱子节点顺序，因为博弈树中倒推值最优的点不止有一个，如果每次都从棋盘左上角开始生成，会博弈树都选择靠近左上角的点，这有很大的规律性，随机生成可以打破这种规律。

一些思考：“复用已有博弈树的子节点”还是“重新生成博弈树”？

• 复用上一轮博弈树
  • 优点
    • 效率更高：避免重新生成整个博弈树，减少重复计算，尤其在搜索深度较大的情况下，节约了时间和计算资源
    • 状态传递直观：可以保留整个博弈树的上下文，使整个流程更加直观
  • 缺点
    • 新的倒推值不一致：下一回合的搜索深度会扩展更多层，导致重新倒推的节点值可能与原值不一致，这可能会导致剪枝流程更加复杂
    • α-β剪枝的副作用：原博弈树中的剪枝可能限制了一些分支的探索，而新的搜索深度会重新探索这些分支，导致结果发生变化，并且在新的搜索中对子节点进行补充时还需要考虑原有子结点的值，处理十分麻烦
• 重新生成博弈树
  • 优点
    • 实现简单：不需要处理博弈树复用的复杂逻辑，更加直观
    • 状态清晰：避免由于同步错误导致的潜在问题，例如子节点状态错误或未完全更新的情况
  • 缺点
    • 效率较低：每回合需要重新计算整个博弈树，无法利用之前的搜索结果，可能浪费计算资源

在进行了综合考虑和尝试后，我发现复用的实现过于复杂，只有在生成完整的博弈树（指深度达到最大）时，复用才会体现出优势，此时的倒推值都是准确的，但是实际上生成完整的博弈树代价十分巨大，复用不完整的博弈树带来的逻辑处理复杂程度远大于重新生成博弈树，所以我选择后者。

各模块代码实现

基本数据结构

棋盘相关

// 棋盘大小
const int BOARD_SIZE = 5;

// 棋盘位置权重
const int POSITION_WEIGHT[BOARD_SIZE][BOARD_SIZE] = {
    {2, 1, 1, 1, 2},
    {1, 2, 2, 2, 1},
    {1, 2, 3, 2, 1},
    {1, 2, 2, 2, 1},
    {2, 1, 1, 1, 2},
};

// 棋盘状态/当前玩家
enum Player {
    EMPTY = 0,    // 空位
    PLAYER_X = 1, // 玩家1
    PLAYER_O = 2  // 玩家2
};

// 棋盘结构
struct Board {
    int grid[BOARD_SIZE][BOARD_SIZE];
  
    // ...（功能函数，之后补充）
}

博弈树节点结构

// 博弈树节点结构
struct Node {
    Board board;                     // 当前棋盘状态
    Player currentPlayer;            // 当前行动方 (此时还未下棋)
    int value;                       // 节点的估值
    vector<Node*> children;          // 子节点列表
    int alpha;                       // α 值（下界）
    int beta;                        // β 值（上界）

    // 构造函数
    Node(Board b, Player player)
        : board(b), currentPlayer(player), value(0), alpha(INT_MIN), beta(INT_MAX) {}
}

记录游戏当前状态

Player currentPlayer; // 当前下棋的玩家
Board currentBoard; // 当前棋局

功能函数实现

棋盘功能函数

// 初始化棋盘为空
void initialize() {
    for (int i = 0; i < BOARD_SIZE; ++i) {
        for (int j = 0; j < BOARD_SIZE; ++j) {
            grid[i][j] = EMPTY;
        }
    }
}

// 打印棋盘
void print() const {
    for (int i = 0; i < BOARD_SIZE; ++i) {
        cout << "  ";
        for (int j = 0; j < BOARD_SIZE; ++j) {
            if (grid[i][j] == EMPTY) cout << ". ";
            else if (grid[i][j] == PLAYER_X) cout << "X ";
            else if (grid[i][j] == PLAYER_O) cout << "O ";
        }
        cout << endl;
    }
    cout << endl;
}

// 判断棋盘是否已满
bool isFull() const {
    for (int i = 0; i < BOARD_SIZE; ++i) {
        for (int j = 0; j < BOARD_SIZE; ++j) {
            if (grid[i][j] == EMPTY) {
                return false;
            }
        }
    }
    return true;
}

// 检查胜负
int checkWinner() const {
    // 检查行、列和对角线是否有连成5个相同棋子的情况
    for (int i = 0; i < BOARD_SIZE; ++i) {
        // 检查行
        if (grid[i][0] != EMPTY &&
            grid[i][0] == grid[i][1] &&
            grid[i][0] == grid[i][2] &&
            grid[i][0] == grid[i][3] &&
            grid[i][0] == grid[i][4]) {
            return grid[i][0];
        }
        // 检查列
        if (grid[0][i] != EMPTY &&
            grid[0][i] == grid[1][i] &&
            grid[0][i] == grid[2][i] &&
            grid[0][i] == grid[3][i] &&
            grid[0][i] == grid[4][i]) {
            return grid[0][i];
        }
    }

    // 主对角线方向
    if (grid[0][0] != EMPTY &&
        grid[0][0] == grid[1][1] &&
        grid[0][0] == grid[2][2] &&
        grid[0][0] == grid[3][3] &&
        grid[0][0] == grid[4][4]) {
        return grid[0][0];
    }
    // 副对角线方向
    if (grid[4][0] != EMPTY &&
        grid[4][0] == grid[3][1] &&
        grid[4][0] == grid[2][2] &&
        grid[4][0] == grid[1][3] &&
        grid[4][0] == grid[0][4]) {
        return grid[4][0];
    }

    // 未分胜负
    return EMPTY;
}

// 转换棋盘为字符串表示，用于去重
string toString() {
    char result[BOARD_SIZE * BOARD_SIZE * 2];
    int index = 0;
    for (int i = 0; i < BOARD_SIZE; ++i) {
        for (int j = 0; j < BOARD_SIZE; ++j) {
            result[index++] = '0' + grid[i][j];
        }
    }
    return string(result, index);
}

// 获取棋盘的所有对称形式（水平对称、垂直对称、主/副对角对称、旋转对称）
vector<Board> getSymmetries() {
    vector<Board> symmetries;

    // 关于水平线对称
    Board horizontal;
    for (int i = 0; i < BOARD_SIZE; ++i) {
        for (int j = 0; j < BOARD_SIZE; ++j) {
            horizontal.grid[i][j] = grid[BOARD_SIZE - i - 1][j];
        }
    }
    symmetries.push_back(horizontal);

    // 关于竖直线对称
    Board vertical;
    for (int i = 0; i < BOARD_SIZE; ++i) {
        for (int j = 0; j < BOARD_SIZE; ++j) {
            vertical.grid[i][j] = grid[i][BOARD_SIZE - j - 1];
        }
    }
    symmetries.push_back(vertical);

    // 关于主对角线对称
    Board main_diag;
    for (int i = 0; i < BOARD_SIZE; ++i) {
        for (int j = 0; j < BOARD_SIZE; ++j) {
            main_diag.grid[i][j] = grid[j][i];
        }
    }
    symmetries.push_back(main_diag);

    // 关于副对角线对称
    Board anti_diag;
    for (int i = 0; i < BOARD_SIZE; ++i) {
        for (int j = 0; j < BOARD_SIZE; ++j) {
            anti_diag.grid[i][j] = grid[BOARD_SIZE - j - 1][BOARD_SIZE - i - 1];
        }
    }
    symmetries.push_back(anti_diag);

    // 旋转90度
    Board rotated_90;
    for (int i = 0; i < BOARD_SIZE; ++i) {
        for (int j = 0; j < BOARD_SIZE; ++j) {
            rotated_90.grid[i][j] = grid[BOARD_SIZE - j - 1][i];
        }
    }
    symmetries.push_back(rotated_90);

    // 旋转180度
    Board rotated_180;
    for (int i = 0; i < BOARD_SIZE; ++i) {
        for (int j = 0; j < BOARD_SIZE; ++j) {
            rotated_180.grid[i][j] = grid[BOARD_SIZE - i - 1][BOARD_SIZE - j - 1];
        }
    }
    symmetries.push_back(rotated_180);

    // 旋转270度
    Board rotated_270;
    for (int i = 0; i < BOARD_SIZE; ++i) {
        for (int j = 0; j < BOARD_SIZE; ++j) {
            rotated_270.grid[i][j] = grid[j][BOARD_SIZE - i - 1];
        }
    }
    symmetries.push_back(rotated_270);

    return symmetries;
}

// 收集所有空格子的位置，返回这些位置的下标（乱序）
vector<pair<int, int>> getEmptyPosition() {
    vector<pair<int, int>> emptyPos;
    for (int i = 0; i < BOARD_SIZE; ++i) {
        for (int j = 0; j < BOARD_SIZE; ++j) {
            if (grid[i][j] == EMPTY) {
                emptyPos.emplace_back(i, j);
            }
        }
    }
    // 随机打乱空格子的位置
    shuffle(emptyPos.begin(), emptyPos.end(), global_re);
    return emptyPos;
}

动态改变搜索深度

// 根据游戏阶段动态改变搜索深度
int dynamicDepth(const Board& board) {
    int emptyPosNum = 0;
    for (int i = 0; i < BOARD_SIZE; ++i) {
        for (int j = 0; j < BOARD_SIZE; ++j) {
            if (board.grid[i][j] == EMPTY) {
                ++emptyPosNum;
            }
        }
    }
    if (emptyPosNum > 20) return 2; // 游戏前期
    if (emptyPosNum > 15) return 4; // 游戏中期
    if (emptyPosNum > 10) return 6; // 游戏中后期
    return min(emptyPosNum, 8); // 游戏后期
}

动态生成子节点

// 为当前节点生成子节点
void getChildren() {
    Player nextPlayer = (currentPlayer == PLAYER_X) ? PLAYER_O : PLAYER_X;
    unordered_set<string> symBoardGroup; // 用于去重，避免生成重复的子节点

    // 遍历空格子
    for (const auto& pos : board.getEmptyPosition()) {
        int i = pos.first, j = pos.second;
        Board newBoard = board;
        newBoard.grid[i][j] = currentPlayer;
        // 检查新棋盘布局是否已在本轮遍历的重复检测组中
        if (symBoardGroup.find(newBoard.toString()) == symBoardGroup.end()) {
            // 如果不存在重复，将其和其对称组添加到重复检测组内
            symBoardGroup.insert(newBoard.toString());
            vector<Board> symmetries = newBoard.getSymmetries();
            for (Board& sym : symmetries) {
                symBoardGroup.insert(sym.toString());
            }
            // 添加新子节点
            children.push_back(new Node(newBoard, nextPlayer));
        }
    }
}

估值函数

// 判断是否是完全空的行、列或对角线
static bool isWinLine(const Board& board, Player player, int dx, int dy, int x_start, int y_start) {
    int opponent = (player == PLAYER_X) ? PLAYER_O : PLAYER_X;
    for (int step = 0; step < BOARD_SIZE; ++step) {
        int x = x_start + step * dx;
        int y = y_start + step * dy;
        if (board.grid[x][y] == opponent) {
            return false; // 存在对方棋子，非可赢行
        }
    }
    return true; // 全空或仅存在自己的棋子
}

// 计算当前棋局对双方而言可以获胜的直线的数量
static pair<int, int> calWinLine(const Board& board) {
    // 统计可赢的行、列和对角线
    int maxLines = 0, minLines = 0;
    // 检查行
    for (int i = 0; i < BOARD_SIZE; ++i) {
        if (isWinLine(board, PLAYER_X, 0, 1, i, 0)) ++maxLines;
        if (isWinLine(board, PLAYER_O, 0, 1, i, 0)) ++minLines;
    }
    // 检查列
    for (int j = 0; j < BOARD_SIZE; ++j) {
        if (isWinLine(board, PLAYER_X, 1, 0, 0, j)) ++maxLines;
        if (isWinLine(board, PLAYER_O, 1, 0, 0, j)) ++minLines;
    }
    // 检查主对角线
    if (isWinLine(board, PLAYER_X, 1, 1, 0, 0)) ++maxLines;
    if (isWinLine(board, PLAYER_O, 1, 1, 0, 0)) ++minLines;
    // 检查次对角线
    if (isWinLine(board, PLAYER_X, 1, -1, 0, BOARD_SIZE - 1)) ++maxLines;
    if (isWinLine(board, PLAYER_O, 1, -1, 0, BOARD_SIZE - 1)) ++minLines;

    return { maxLines, minLines };
}

// 估值函数：e(P)=e(MAX可胜利的行、列或对角线的总数)-e(MIN可胜利的行、列或对角线的总数)
static int evaluate(const Node* node, int depth) {
    // 检查是否是终止节点
    int winner = node->board.checkWinner();
    if (winner == PLAYER_X) return INT_MAX / 2 + depth; // 本节点为MAX胜局
    if (winner == PLAYER_O) return INT_MIN / 2 - depth; // 本节点为MIN胜局


    int posWeight = 0;
    for (int i = 0; i < BOARD_SIZE; ++i) {
        for (int j = 0; j < BOARD_SIZE; ++j) {
            if (node->board.grid[i][j] == PLAYER_X) {
                posWeight += POSITION_WEIGHT[i][j];
            }
            else if (node->board.grid[i][j] == PLAYER_O) {
                posWeight -= POSITION_WEIGHT[i][j];
            }
        }
    }

    pair<int, int> lines = calWinLine(node->board);

    // 返回评估值
    return posWeight + lines.first - lines.second;
}

博弈树搜索入口/AI玩家移动逻辑

函数makeChoiceAI控制AI移动，它是生成博弈树的入口。

// AI玩家移动
void makeChoiceAI() {
    cout << "====== " << ((currentPlayer == PLAYER_X) ? "玩家 1(AI) " : "玩家 2(AI) ") << "的回合 ======" << endl;
    cout << "思考中..." << endl;
    // 创建博弈树根节点
    Node* root = new Node(currentBoard, currentPlayer);
    // 使用极小极大搜索选择最佳落子，dynamicDepth是根据回合数动态改变搜索深度的函数，之后的步骤会提供实现
    minimax(root, dynamicDepth(currentBoard), INT_MIN, INT_MAX);
    // 选择最优子节点
    for (Node* child : root->children) {
        if (child->value == root->value) {
            cout << "思考完毕。" << endl;
            currentBoard = child->board; // 选择评估值最优的子节点
            currentBoard.print();  // 打印当前棋盘
            delete root;
            break;
        }
    }
}

博弈树搜索主函数

// 带α-β剪枝的极小极大搜索
static int minimax(Node* node, int depth, int preAlpha, int preBeta) {
    // 有获胜者，或棋盘已满，或已达到本轮搜索最大深度，则开始计算倒推值
    if (node->board.checkWinner() != EMPTY || node->board.isFull() || depth == 0) {
        node->value = evaluate(node, depth); // !!!注意这里要更新叶子节点的倒推值
        return node->value;
    }

    // 往下生成一层子节点
    if (node->children.empty()) node->getChildren();

    // MAX节点：该层是MIN刚下完棋的局面，意为轮到MAX的回合，其子结点是MAX所有可能出棋情况
    if (node->currentPlayer == PLAYER_X) {
        node->value = INT_MIN;
        auto it = node->children.begin();
        while (it != node->children.end()) {
            Node* child = *it;
            // 更新倒推值：MAX层节点从子节点选择最大的值
            node->value = max(node->value, minimax(child, depth - 1, node->alpha, node->beta));
            node->alpha = node->value; // 更新 α 值

            // β剪枝：当前节点的 α 大于等于父节点 β
            if (node->alpha >= preBeta) {
                // 删除剩余的子节点
                for (auto delIt = it + 1; delIt != node->children.end(); ++delIt) {
                    delete* delIt;
                }
                // 移除未访问的子节点
                node->children.erase(it + 1, node->children.end());
                break;
            }
            ++it; // 正常继续访问下一个子节点
        }
        return node->value;
    }
    // MIN节点：该层是MAX刚下完棋的局面，意为轮到MIN的回合，其子结点是MIN所有可能出棋情况
    else {
        node->value = INT_MAX;
        auto it = node->children.begin();
        while (it != node->children.end()) {
            Node* child = *it;
            // 更新倒推值：MIN层节点从子节点选择最小的值
            node->value = min(node->value, minimax(child, depth - 1, node->alpha, node->beta));
            node->beta = node->value; // 更新 β 值

            // α剪枝：当前节点的 β 小于等于父节点 α
            if (node->beta <= preAlpha) {
                // 删除剩余的子节点
                for (auto delIt = it + 1; delIt != node->children.end(); ++delIt) {
                    delete* delIt;
                }
                // 移除未访问的子节点
                node->children.erase(it + 1, node->children.end());
                break;
            }
            ++it; // 正常继续访问下一个子节点
        }
        return node->value;
    }
}

游戏流程控制逻辑

人类玩家移动&随机移动逻辑

// 人类玩家移动
void makeChoiceHuman() {
    cout << "======== " << ((currentPlayer == PLAYER_X) ? "玩家 1 " : "玩家 2 ") << "的回合 ========" << endl;
    while (true) {
        cout << "请输入你的落子位置: ";
        cin.ignore((numeric_limits<streamsize>::max)(), '\n'); // 清空输入缓冲区
        int row, col;
        cin >> row >> col;
        if (row < 1 || col < 1 || row > 5 || col > 5) {
            cout << "无效位置，请重试！" << endl;
        }
        else if (currentBoard.grid[--row][--col] == EMPTY) {
            currentBoard.grid[row][col] = currentPlayer;
            cout << "你的棋落在了 (" << row + 1 << "," << col + 1 << ") 上。" << endl;
            currentBoard.print();  // 打印当前棋盘
            break;
        }
        else cout << "该格已被占用，请重试！" << endl;
    }
}

// 随机玩家移动
void makeChoiceRandom() {
    cout << "====== " << ((currentPlayer == PLAYER_X) ? "玩家 1(随机) " : "玩家 2(随机) ") << "的回合 ======" << endl;
    cout << "随机落子。" << endl;
    // 收集所有空位置（乱序）
    vector<pair<int, int>> emptyPos = currentBoard.getEmptyPosition();
    // 执行移动
    currentBoard.grid[emptyPos[0].first][emptyPos[0].second] = currentPlayer;
    // 打印当前棋盘
    currentBoard.print();
}

游戏运行主逻辑

// 游戏运行逻辑
void play() {
    currentBoard.initialize(); // 初始化棋盘
    currentPlayer = PLAYER_X; // 玩家 1 先手

    cout << "选择玩家: " << endl;
    cout << "A. 玩家 1 (先手)    B. 玩家 2 (后手)    C.双AI对战    D.AI vs 随机" << endl;
    cout << "请输入 A, B, C 或 D : ";
    char gameMode;
    while (true) {
        cin >> gameMode;
        if (gameMode > 'Z') gameMode -= 32;
        if (gameMode == 'A' || gameMode == 'B' || gameMode == 'C' || gameMode == 'D') break;
        cout << "输入无效！请重新输入: ";
    }
    if (gameMode == 'A' || gameMode == 'B') {
        cout << "你是玩家 " << ((gameMode == 'A') ? "1 。" : "2 。") << endl;
    }
    else if (gameMode == 'C') {
        cout << "本局游戏为AI对战。" << endl;
    }
    else {
        cout << "本局游戏为AI vs 随机。" << endl;
    }

    // 打印当前棋盘
    currentBoard.print();

    while (true) {
        Sleep(500);

        // 检查是否有胜者或平局
        int winner = currentBoard.checkWinner();
        if (winner == PLAYER_X) {
            cout << "玩家 1 获胜!" << endl;
            //win1++;
            break;
        }
        else if (winner == PLAYER_O) {
            cout << "玩家 2 获胜!" << endl;
            //win2++;
            break;
        }
        else if (currentBoard.isFull()) {
            cout << "平局!" << endl;
            //tied++;
            break;
        }
        else {
            pair<int, int> lines = GameTree::calWinLine(currentBoard);
            if (lines.first == 0 && lines.second == 0) {
                cout << "陷入僵局!" << endl;
                //tied++;
                break;
            }
        }

        // 根据游戏模式选择玩家操控模式
        switch (gameMode) {
        case 'A':
            if (currentPlayer == PLAYER_X) makeChoiceHuman();
            else makeChoiceAI();
            break;
        case 'B':
            if (currentPlayer == PLAYER_X) makeChoiceAI();
            else makeChoiceHuman();
            break;
        case 'C':
            if (currentPlayer == PLAYER_X) makeChoiceAI();
            else makeChoiceAI();
            break;
        case 'D':
            if (currentPlayer == PLAYER_X) makeChoiceAI();
            else makeChoiceRandom();
            break;
        default:
            break;
        }

        // 切换玩家
        currentPlayer = (currentPlayer == PLAYER_X) ? PLAYER_O : PLAYER_X;
    }
}

完整代码

#include <iostream>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <climits>
#include <unordered_set>
#include <algorithm>
#include <windows.h>
#include <random>
#include <chrono>
using namespace std;

// 随机数引擎
auto seed = chrono::steady_clock::now().time_since_epoch().count();
mt19937 global_re(seed);

//int win1, win2, tied; // 批量测试时记录每次比赛的结果

// 棋盘大小
const int BOARD_SIZE = 5;

// 棋盘位置权重
const int POSITION_WEIGHT[BOARD_SIZE][BOARD_SIZE] = {
    {2, 1, 1, 1, 2},
    {1, 2, 2, 2, 1},
    {1, 2, 3, 2, 1},
    {1, 2, 2, 2, 1},
    {2, 1, 1, 1, 2},
};

// 棋盘状态/当前玩家
enum Player {
    EMPTY = 0,    // 空位
    PLAYER_X = 1, // 玩家1
    PLAYER_O = 2  // 玩家2
};

// 棋盘结构
struct Board {
    int grid[BOARD_SIZE][BOARD_SIZE]; // 棋盘5x5

    // 初始化棋盘为空
    void initialize() {
        for (int i = 0; i < BOARD_SIZE; ++i) {
            for (int j = 0; j < BOARD_SIZE; ++j) {
                grid[i][j] = EMPTY;
            }
        }
    }

    // 打印棋盘
    void print() const {
        for (int i = 0; i < BOARD_SIZE; ++i) {
            cout << "  ";
            for (int j = 0; j < BOARD_SIZE; ++j) {
                if (grid[i][j] == EMPTY) cout << ". ";
                else if (grid[i][j] == PLAYER_X) cout << "X ";
                else if (grid[i][j] == PLAYER_O) cout << "O ";
            }
            cout << endl;
        }
        cout << endl;
    }

    // 判断棋盘是否已满
    bool isFull() const {
        for (int i = 0; i < BOARD_SIZE; ++i) {
            for (int j = 0; j < BOARD_SIZE; ++j) {
                if (grid[i][j] == EMPTY) {
                    return false;
                }
            }
        }
        return true;
    }

    // 检查胜负
    int checkWinner() const {
        // 检查行、列和对角线是否有连成5个相同棋子的情况
        for (int i = 0; i < BOARD_SIZE; ++i) {
            // 检查行
            if (grid[i][0] != EMPTY &&
                grid[i][0] == grid[i][1] &&
                grid[i][0] == grid[i][2] &&
                grid[i][0] == grid[i][3] &&
                grid[i][0] == grid[i][4]) {
                return grid[i][0];
            }
            // 检查列
            if (grid[0][i] != EMPTY &&
                grid[0][i] == grid[1][i] &&
                grid[0][i] == grid[2][i] &&
                grid[0][i] == grid[3][i] &&
                grid[0][i] == grid[4][i]) {
                return grid[0][i];
            }
        }

        // 主对角线方向
        if (grid[0][0] != EMPTY &&
            grid[0][0] == grid[1][1] &&
            grid[0][0] == grid[2][2] &&
            grid[0][0] == grid[3][3] &&
            grid[0][0] == grid[4][4]) {
            return grid[0][0];
        }
        // 副对角线方向
        if (grid[4][0] != EMPTY &&
            grid[4][0] == grid[3][1] &&
            grid[4][0] == grid[2][2] &&
            grid[4][0] == grid[1][3] &&
            grid[4][0] == grid[0][4]) {
            return grid[4][0];
        }

        // 未分胜负
        return EMPTY;
    }

    // 转换棋盘为字符串表示，用于去重
    string toString() {
        char result[BOARD_SIZE * BOARD_SIZE * 2];
        int index = 0;
        for (int i = 0; i < BOARD_SIZE; ++i) {
            for (int j = 0; j < BOARD_SIZE; ++j) {
                result[index++] = '0' + grid[i][j];
            }
        }
        return string(result, index);
    }

    // 获取棋盘的所有对称形式（水平对称、垂直对称、主/副对角对称、旋转对称）
    vector<Board> getSymmetries() {
        vector<Board> symmetries;

        // 关于水平线对称
        Board horizontal;
        for (int i = 0; i < BOARD_SIZE; ++i) {
            for (int j = 0; j < BOARD_SIZE; ++j) {
                horizontal.grid[i][j] = grid[BOARD_SIZE - i - 1][j];
            }
        }
        symmetries.push_back(horizontal);

        // 关于竖直线对称
        Board vertical;
        for (int i = 0; i < BOARD_SIZE; ++i) {
            for (int j = 0; j < BOARD_SIZE; ++j) {
                vertical.grid[i][j] = grid[i][BOARD_SIZE - j - 1];
            }
        }
        symmetries.push_back(vertical);

        // 关于主对角线对称
        Board main_diag;
        for (int i = 0; i < BOARD_SIZE; ++i) {
            for (int j = 0; j < BOARD_SIZE; ++j) {
                main_diag.grid[i][j] = grid[j][i];
            }
        }
        symmetries.push_back(main_diag);

        // 关于副对角线对称
        Board anti_diag;
        for (int i = 0; i < BOARD_SIZE; ++i) {
            for (int j = 0; j < BOARD_SIZE; ++j) {
                anti_diag.grid[i][j] = grid[BOARD_SIZE - j - 1][BOARD_SIZE - i - 1];
            }
        }
        symmetries.push_back(anti_diag);

        // 旋转90度
        Board rotated_90;
        for (int i = 0; i < BOARD_SIZE; ++i) {
            for (int j = 0; j < BOARD_SIZE; ++j) {
                rotated_90.grid[i][j] = grid[BOARD_SIZE - j - 1][i];
            }
        }
        symmetries.push_back(rotated_90);

        // 旋转180度
        Board rotated_180;
        for (int i = 0; i < BOARD_SIZE; ++i) {
            for (int j = 0; j < BOARD_SIZE; ++j) {
                rotated_180.grid[i][j] = grid[BOARD_SIZE - i - 1][BOARD_SIZE - j - 1];
            }
        }
        symmetries.push_back(rotated_180);

        // 旋转270度
        Board rotated_270;
        for (int i = 0; i < BOARD_SIZE; ++i) {
            for (int j = 0; j < BOARD_SIZE; ++j) {
                rotated_270.grid[i][j] = grid[j][BOARD_SIZE - i - 1];
            }
        }
        symmetries.push_back(rotated_270);

        return symmetries;
    }

    // 收集所有空格子的位置，返回这些位置的下标（乱序）
    vector<pair<int, int>> getEmptyPosition() {
        vector<pair<int, int>> emptyPos;
        for (int i = 0; i < BOARD_SIZE; ++i) {
            for (int j = 0; j < BOARD_SIZE; ++j) {
                if (grid[i][j] == EMPTY) {
                    emptyPos.emplace_back(i, j);
                }
            }
        }
        // 随机打乱空格子的位置
        shuffle(emptyPos.begin(), emptyPos.end(), global_re);
        return emptyPos;
    }
};

// 博弈树节点结构
struct Node {
    Board board;                     // 当前棋盘状态
    Player currentPlayer;            // 当前行动方 (此时还未下棋)
    int value;                       // 节点的估值
    vector<Node*> children;          // 子节点列表
    int alpha;                       // α 值（下界）
    int beta;                        // β 值（上界）

    // 构造函数
    Node(Board b, Player player)
        : board(b), currentPlayer(player), value(0), alpha(INT_MIN), beta(INT_MAX) {}

    // 析构函数释放子节点内存
    ~Node() {
        for (auto child : children) {
            delete child;
        }
    }

    // 为当前节点生成子节点
    void getChildren() {
        Player nextPlayer = (currentPlayer == PLAYER_X) ? PLAYER_O : PLAYER_X;
        unordered_set<string> symBoardGroup; // 用于去重，避免生成重复的子节点

        // 遍历空格子
        for (const auto& pos : board.getEmptyPosition()) {
            int i = pos.first, j = pos.second;
            Board newBoard = board;
            newBoard.grid[i][j] = currentPlayer;
            // 检查新棋盘布局是否已在本轮遍历的重复检测组中
            if (symBoardGroup.find(newBoard.toString()) == symBoardGroup.end()) {
                // 如果不存在重复，将其和其对称组添加到重复检测组内
                symBoardGroup.insert(newBoard.toString());
                vector<Board> symmetries = newBoard.getSymmetries();
                for (Board& sym : symmetries) {
                    symBoardGroup.insert(sym.toString());
                }
                // 添加新子节点
                children.push_back(new Node(newBoard, nextPlayer));
            }
        }
    }
};

// 博弈树算法类
class GameTree {
public:
    // 判断是否是完全空的行、列或对角线
    static bool isWinLine(const Board& board, Player player, int dx, int dy, int x_start, int y_start) {
        int opponent = (player == PLAYER_X) ? PLAYER_O : PLAYER_X;
        for (int step = 0; step < BOARD_SIZE; ++step) {
            int x = x_start + step * dx;
            int y = y_start + step * dy;
            if (board.grid[x][y] == opponent) {
                return false; // 存在对方棋子，非可赢行
            }
        }
        return true; // 全空或仅存在自己的棋子
    }

    // 计算当前棋局对双方而言可以获胜的直线的数量
    static pair<int, int> calWinLine(const Board& board) {
        // 统计可赢的行、列和对角线
        int maxLines = 0, minLines = 0;
        // 检查行
        for (int i = 0; i < BOARD_SIZE; ++i) {
            if (isWinLine(board, PLAYER_X, 0, 1, i, 0)) ++maxLines;
            if (isWinLine(board, PLAYER_O, 0, 1, i, 0)) ++minLines;
        }
        // 检查列
        for (int j = 0; j < BOARD_SIZE; ++j) {
            if (isWinLine(board, PLAYER_X, 1, 0, 0, j)) ++maxLines;
            if (isWinLine(board, PLAYER_O, 1, 0, 0, j)) ++minLines;
        }
        // 检查主对角线
        if (isWinLine(board, PLAYER_X, 1, 1, 0, 0)) ++maxLines;
        if (isWinLine(board, PLAYER_O, 1, 1, 0, 0)) ++minLines;
        // 检查次对角线
        if (isWinLine(board, PLAYER_X, 1, -1, 0, BOARD_SIZE - 1)) ++maxLines;
        if (isWinLine(board, PLAYER_O, 1, -1, 0, BOARD_SIZE - 1)) ++minLines;

        return { maxLines, minLines };
    }

    // 估值函数：e(P)=e(MAX可胜利的行、列或对角线的总数)-e(MIN可胜利的行、列或对角线的总数)
    static int evaluate(const Node* node, int depth) {
        // 检查是否是终止节点
        int winner = node->board.checkWinner();
        if (winner == PLAYER_X) return INT_MAX / 2 + depth; // 本节点为MAX胜局
        if (winner == PLAYER_O) return INT_MIN / 2 - depth; // 本节点为MIN胜局


        int posWeight = 0;
        for (int i = 0; i < BOARD_SIZE; ++i) {
            for (int j = 0; j < BOARD_SIZE; ++j) {
                if (node->board.grid[i][j] == PLAYER_X) {
                    posWeight += POSITION_WEIGHT[i][j];
                }
                else if (node->board.grid[i][j] == PLAYER_O) {
                    posWeight -= POSITION_WEIGHT[i][j];
                }
            }
        }

        pair<int, int> lines = calWinLine(node->board);

        // 返回评估值
        return posWeight + lines.first - lines.second;
    }

    // 带α-β剪枝的极小极大搜索
    static int minimax(Node* node, int depth, int preAlpha, int preBeta) {
        // 有获胜者，或棋盘已满，或已达到本轮搜索最大深度，则开始计算倒推值
        if (node->board.checkWinner() != EMPTY || node->board.isFull() || depth == 0) {
            node->value = evaluate(node, depth); // !!!注意这里要更新叶子节点的倒推值
            return node->value;
        }

        // 往下生成一层子节点
        if (node->children.empty()) node->getChildren();

        // MAX节点：该层是MIN刚下完棋的局面，意为轮到MAX的回合，其子结点是MAX所有可能出棋情况
        if (node->currentPlayer == PLAYER_X) {
            node->value = INT_MIN;
            auto it = node->children.begin();
            while (it != node->children.end()) {
                Node* child = *it;
                // 更新倒推值：MAX层节点从子节点选择最大的值
                node->value = max(node->value, minimax(child, depth - 1, node->alpha, node->beta));
                node->alpha = node->value; // 更新 α 值

                // β剪枝：当前节点的 α 大于等于父节点 β
                if (node->alpha >= preBeta) {
                    // 删除剩余的子节点
                    for (auto delIt = it + 1; delIt != node->children.end(); ++delIt) {
                        delete* delIt;
                    }
                    // 移除未访问的子节点
                    node->children.erase(it + 1, node->children.end());
                    break;
                }
                ++it; // 正常继续访问下一个子节点
            }
            return node->value;
        }
        // MIN节点：该层是MAX刚下完棋的局面，意为轮到MIN的回合，其子结点是MIN所有可能出棋情况
        else {
            node->value = INT_MAX;
            auto it = node->children.begin();
            while (it != node->children.end()) {
                Node* child = *it;
                // 更新倒推值：MIN层节点从子节点选择最小的值
                node->value = min(node->value, minimax(child, depth - 1, node->alpha, node->beta));
                node->beta = node->value; // 更新 β 值

                // α剪枝：当前节点的 β 小于等于父节点 α
                if (node->beta <= preAlpha) {
                    // 删除剩余的子节点
                    for (auto delIt = it + 1; delIt != node->children.end(); ++delIt) {
                        delete* delIt;
                    }
                    // 移除未访问的子节点
                    node->children.erase(it + 1, node->children.end());
                    break;
                }
                ++it; // 正常继续访问下一个子节点
            }
            return node->value;
        }
    }
};

// 游戏运行逻辑类
class GameUtil {
public:
    Player currentPlayer; // 当前下棋的玩家
    Board currentBoard; // 当前棋局

    void intro() {
        cout << "============== 5x5一字棋游戏 ==============" << endl;
        cout << "================ 游戏介绍 =================" << endl;
        cout << "    这是一个棋盘为5x5的一字棋游戏，玩家1的棋子为X，玩家2的棋子为O，" << endl;
        cout << "    当一方的其中5个棋子在横向、纵向或斜对角线上连成一条线时，他将赢得胜利。" << endl;
        cout << "================== 教程 ===================" << endl;
        cout << "最开始时，棋盘如下图所示：" << endl;
        Board* tmp = new Board();
        tmp->initialize();
        tmp->print();
        cout << "当出现 \"请输入你的落子位置:\" 提示时：" << endl;
        cout << "如果你要将棋子下在第2行第5列，则输入 \"2 5\" 然后回车" << endl;
        cout << "以下是一个示例：" << endl;
        cout << "----------------------------------------" << endl;
        cout << "请输入你的落子位置: 2 5" << endl;
        cout << "你的棋落在了 (2,5) 上。" << endl;
        tmp->grid[1][4] = PLAYER_X;
        tmp->print();
        delete tmp;
        cout << "----------------------------------------" << endl;
    }

    // 根据游戏阶段动态改变搜索深度
    int dynamicDepth(const Board& board) {
        int emptyPosNum = 0;
        for (int i = 0; i < BOARD_SIZE; ++i) {
            for (int j = 0; j < BOARD_SIZE; ++j) {
                if (board.grid[i][j] == EMPTY) {
                    ++emptyPosNum;
                }
            }
        }
        if (emptyPosNum > 20) return 2; // 游戏前期
        if (emptyPosNum > 15) return 4; // 游戏中期
        if (emptyPosNum > 10) return 6; // 游戏中后期
        return min(emptyPosNum, 8); // 游戏后期
    }

    // AI玩家移动
    void makeChoiceAI() {
        cout << "====== " << ((currentPlayer == PLAYER_X) ? "玩家 1(AI) " : "玩家 2(AI) ") << "的回合 ======" << endl;
        cout << "思考中..." << endl;
        // 创建博弈树根节点
        Node* root = new Node(currentBoard, currentPlayer);
        // 使用极小极大搜索选择最佳落子
        GameTree::minimax(root, dynamicDepth(currentBoard), INT_MIN, INT_MAX);
        // 选择最优子节点
        for (Node* child : root->children) {
            if (child->value == root->value) {
                cout << "思考完毕。" << endl;
                currentBoard = child->board; // 选择评估值最优的子节点
                currentBoard.print();  // 打印当前棋盘
                delete root;
                break;
            }
        }
    }

    // 人类玩家移动
    void makeChoiceHuman() {
        cout << "======== " << ((currentPlayer == PLAYER_X) ? "玩家 1 " : "玩家 2 ") << "的回合 ========" << endl;
        while (true) {
            cout << "请输入你的落子位置: ";
            cin.ignore((numeric_limits<streamsize>::max)(), '\n'); // 清空输入缓冲区
            int row, col;
            cin >> row >> col;
            if (row < 1 || col < 1 || row > 5 || col > 5) {
                cout << "无效位置，请重试！" << endl;
            }
            else if (currentBoard.grid[--row][--col] == EMPTY) {
                currentBoard.grid[row][col] = currentPlayer;
                cout << "你的棋落在了 (" << row + 1 << "," << col + 1 << ") 上。" << endl;
                currentBoard.print();  // 打印当前棋盘
                break;
            }
            else cout << "该格已被占用，请重试！" << endl;
        }
    }

    // 随机玩家移动
    void makeChoiceRandom() {
        cout << "====== " << ((currentPlayer == PLAYER_X) ? "玩家 1(随机) " : "玩家 2(随机) ") << "的回合 ======" << endl;
        cout << "随机落子。" << endl;
        // 收集所有空位置（乱序）
        vector<pair<int, int>> emptyPos = currentBoard.getEmptyPosition();
        // 执行移动
        currentBoard.grid[emptyPos[0].first][emptyPos[0].second] = currentPlayer;
        // 打印当前棋盘
        currentBoard.print();
    }

    // 游戏运行逻辑
    void play() {
        currentBoard.initialize(); // 初始化棋盘
        currentPlayer = PLAYER_X; // 玩家 1 先手

        cout << "选择玩家: " << endl;
        cout << "A. 玩家 1 (先手)    B. 玩家 2 (后手)    C.双AI对战    D.AI vs 随机" << endl;
        cout << "请输入 A, B, C 或 D : ";
        char gameMode;
        while (true) {
            cin >> gameMode;
            if (gameMode > 'Z') gameMode -= 32;
            if (gameMode == 'A' || gameMode == 'B' || gameMode == 'C' || gameMode == 'D') break;
            cout << "输入无效！请重新输入: ";
        }
        if (gameMode == 'A' || gameMode == 'B') {
            cout << "你是玩家 " << ((gameMode == 'A') ? "1 。" : "2 。") << endl;
        }
        else if (gameMode == 'C') {
            cout << "本局游戏为AI对战。" << endl;
        }
        else {
            cout << "本局游戏为AI vs 随机。" << endl;
        }

        // 打印当前棋盘
        currentBoard.print();

        while (true) {
            Sleep(500);

            // 检查是否有胜者或平局
            int winner = currentBoard.checkWinner();
            if (winner == PLAYER_X) {
                cout << "玩家 1 获胜!" << endl;
                //win1++;
                break;
            }
            else if (winner == PLAYER_O) {
                cout << "玩家 2 获胜!" << endl;
                //win2++;
                break;
            }
            else if (currentBoard.isFull()) {
                cout << "平局!" << endl;
                //tied++;
                break;
            }
            else {
                pair<int, int> lines = GameTree::calWinLine(currentBoard);
                if (lines.first == 0 && lines.second == 0) {
                    cout << "陷入僵局!" << endl;
                    //tied++;
                    break;
                }
            }

            // 根据游戏模式选择玩家操控模式
            switch (gameMode) {
            case 'A':
                if (currentPlayer == PLAYER_X) makeChoiceHuman();
                else makeChoiceAI();
                break;
            case 'B':
                if (currentPlayer == PLAYER_X) makeChoiceAI();
                else makeChoiceHuman();
                break;
            case 'C':
                if (currentPlayer == PLAYER_X) makeChoiceAI();
                else makeChoiceAI();
                break;
            case 'D':
                if (currentPlayer == PLAYER_X) makeChoiceAI();
                else makeChoiceRandom();
                break;
            default:
                break;
            }

            // 切换玩家
            currentPlayer = (currentPlayer == PLAYER_X) ? PLAYER_O : PLAYER_X;
        }
    }
};

int main() {
    //int n = 50; // 批量测试50轮
    //int cnt = n;
    //while (cnt--) {
    GameUtil game;
    game.intro();
    cout << "================ 游戏开始 =================" << endl;
    game.play();
    cout << "\n================ 游戏结束 =================\n" << endl;
    //    cout << "一共进行了 " << n - cnt << " 轮游戏, 玩家1胜利: " << win1 << ", 玩家2胜利 : " << win2 << ", 平局 : " << tied << endl;
    //}

    system("pause");
    return 0;
}

实验结果

开局介绍

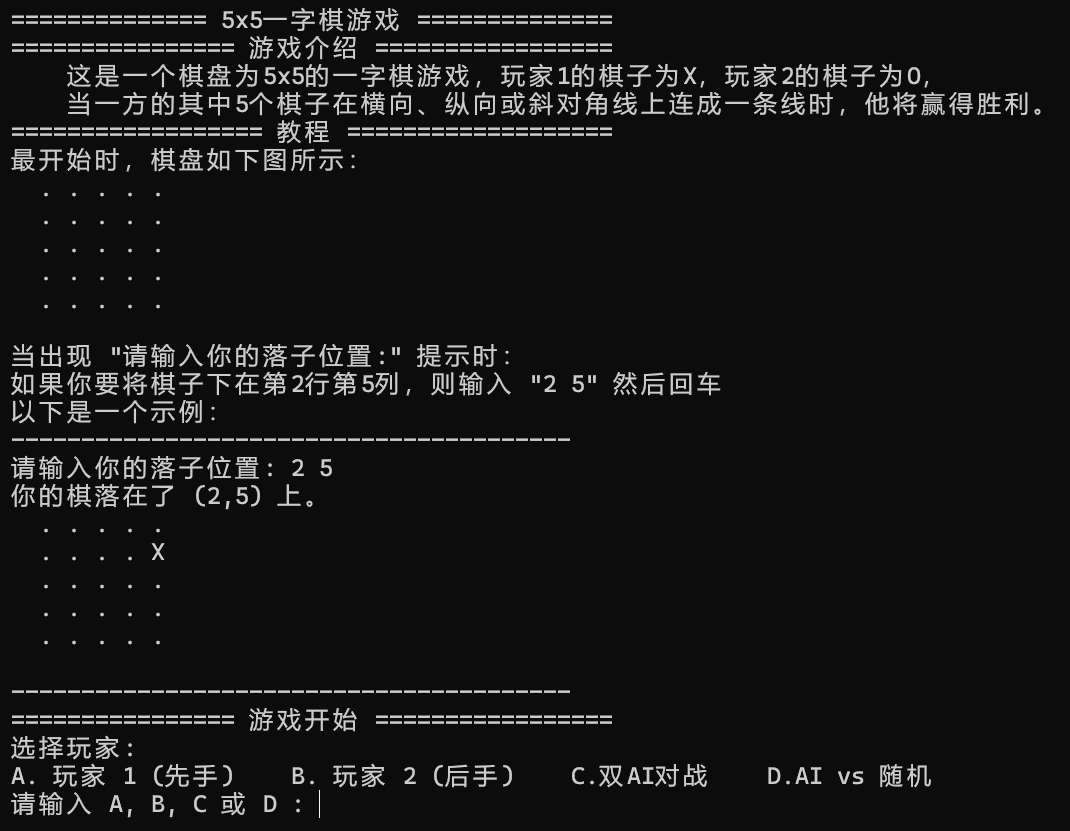
双AI对战

永远是平局。

AI vs 随机

AI不可能输，最多平局。

人类(玩家1) vs AI(玩家2)

人类赢不了，最多平局。

参考文章

• 人工智能第四章博弈树 a-b剪枝
• Alpha-Beta剪枝(Alpha Beta Pruning)
• 博弈树