无人车路径/车速规划实验：A*算法 & 模糊推理 C++代码实现

实验要求

1. A*算法：生成一个 N x N 的二维网格，随机指定一些格子为障碍，左下角有辆车（占一个格子）要去右上角，使用 A* 算法先计算起点到终点的不撞到障碍的最短路径。
2. 模糊推理：计算完后，利用路径上每个点的局部曲率，以及到周围最近障碍的距离来控制车辆的速度。要求使用模糊逻辑建立曲率小，离障碍距离远，车速快三个模糊集合，构建曲率小——车速快的关系矩阵，距离远——车速快的关系矩阵， 根据 A* 路径上每个点实际的曲率和离障碍物的距离，使用模糊推理及规则合成，得到目标在A*搜索到的路径的每个格子的瞬时速度，车辆按瞬时速度从左下到右上沿着 A* 路径行驶。

A*算法：无人车路径规划

前言

状态空间

• 定义：使用“状态”和“操作”表示问题的解决空间，由所有可能的状态和可用操作构成。
• 构成：问题可能具有的初始状态的集合 S ，操作的集合 F ，目标状态的集合 G。

最佳优先搜索

定义

OPEN表节点按估价函数 f(x) 的值排序，选择函数值最小的节点作为下一个被考察的节点。

最佳优先搜索又分为局部最佳优先搜索和全局最佳优先搜索。

局部最佳优先搜索

当一个节点 x 被扩展以后，对每个子节点按 f(x) 的值排序，并从新扩展的子节点中选择估计值最小的节点，作为下一个考察对象。

全局最佳优先搜索

在 OPEN 表中的全部节点中选择一个估价函数值 f(x) 最小的节点，作为下一个考察对象。因为选择的范围是 OPEN 表中的全部节点（而不是新扩展的子节点），所以它称为全局最佳优先搜索。

A* 算法

定义

A*算法是在启发式搜索中使用估价函数 f(n) = g(n) + h(n) 的搜索算法。

其中：

• g(n) 表示从初始结点到任意结点 n 的代价
• h(n) 表示从结点 n 到目标点的启发式评估代价。

h(n) 被称为启发式函数，它告诉 A* 从任意结点 n 到目标结点的最小代价评估值。

A* 算法与 A 算法的区别

A* 算法要求 h(n) ≤ h*(n)，对 h(n) 进行了限制，是优化版的 A 算法。

g(n) 和 h(n) 的比重

• g(n) 的比重越大，搜索方式就越倾向 Dijkstra 算法/广度优先搜索，关注路径的累积代价，确保找到从起点到所有节点的最短路径。
• h(n) 的比重越大，越倾向于最佳优先搜索/深度优先搜索，只关注到目标的估计距离，可能会更快找到一个解，但不一定是最优解。

Dijkstra 算法/广度优先搜索、最佳优先搜索/深度优先搜索的异同点

1. Dijkstra 算法与广度优先搜索

共同点：

• 扩展方式：Dijkstra 算法和广度优先搜索都从起始节点开始，逐层向外扩展。
• 遍历结构：两者都确保在扩展每一层的所有节点之前不会深入到下一层，这使得它们在无权图中都可以找到最短路径。

区别：

• 代价的考量：Dijkstra 算法适用于加权图，优先扩展代价（路径长度）较低的节点，以找到从起点到所有节点的最短路径。而广度优先搜索适用于无权图，直接按照层次顺序扩展节点，找到的路径是层数最少的路径。
• 适用性：Dijkstra 算法可以用于加权图求解最短路径，但广度优先搜索仅适用于无权图的最短路径搜索。

因此，当 Dijkstra 算法用于无权图时，它的行为与广度优先搜索几乎完全一致，因为在无权图中所有边的代价相等，可以看作是广度优先搜索的推广。

2. 最佳优先搜索与深度优先搜索

共同点：

• 倾向快速逼近目标：两者在某些情况下可能会深入到搜索树的较深层级，追求尽早找到目标节点，而不是逐层扩展。

区别：

• 搜索控制依据：最佳优先搜索基于启发式估价函数 h(n)h(n)h(n)，优先扩展离目标估计代价最小的节点。它不保证找到最优解，但能快速逼近目标。深度优先搜索则不依赖启发信息，仅是按照最近生成的节点优先扩展，可能无意中深入错误方向，并且不能保证最优解。
• 应用场景：最佳优先搜索在路径估计信息明确且启发函数有效时效果较好，而深度优先搜索适用于解空间大、且不需要找到最优解的情况，如某些问题的简单解。

总结：最佳优先搜索类似于一种带有“方向感”的深度优先搜索，它利用启发函数来选择路径，并尝试快速达到目标位置，而深度优先搜索则完全不考虑目标距离。

算法流程

基本思想：从初始节点开始，按照 f(n) 值选择最小的节点进行扩展，直到找到目标节点。

1. 数据结构

• 节点结构定义：每个 Node 包含坐标 x 和 y，从起点到当前节点的总代价 f，以及路径代价 g 和启发式估计 h，还有指向父节点的指针 parent。
• 启发式函数 h：heuristic 函数用曼哈顿距离计算从当前节点到目标节点的估算代价。
• OPEN表：openList 用于存储待处理的节点，优先队列将自动根据 f 值对节点排序，优先处理 f 值较小的节点（即总代价最低的节点）。
• CLOSED表：closedList 存储已处理的节点，避免重复访问。

2. A*算法流程

a. 初始化

1. 手动输入网格大小和障碍物数量
2. 随机生成障碍物，并确保起点和终点处没有障碍
3. 创建起点和目标点节点，并将起点加入OPEN表

b. 循环处理

• 若OPEN表不为空，则执行：

  1. 从OPEN表中取出 f 值最小的节点作为当前处理节点 current
  2. 将current放入CLOSED表
  3. 如果 current 是目的地节点，则表示找到路径
     • 通过 parent 回溯路径，将路径存入 path，并返回
  4. 否则，将 current 节点标记为已访问，并进行下一步
  5. 遍历 current 的四个方向邻居节点，生成新节点并计算 g、h 和 f 值，将其加入OPEN表
     • 边界和障碍检查：确保邻居节点可通行
     • CLOSED表检查：若邻居节点已在CLOSED表中，说明已处理过，跳过

• 若OPEN表为空，则说明不可达，跳出循环，返回空 path

c. 输出结果

• 根据 path 输出路线图

欧几里得距离：顶点跟终点之间的直线距离。

曼哈顿距离：两点之间横纵坐标的距离之和。计算的过程只涉及加减法、符号位反转，所以比欧几里得距离更加高效。

各模块代码实现

数据结构定义

节点结构体

#define x first
#define y second
typedef pair<int, int> PII;

// 节点结构体
struct Node {
    int x, y; // 坐标
    int g, h, f; // g为起点到当前节点的代价，h为启发式评估代价，f = g + h 为总代价
    Node* parent; // 指向父节点的指针

    Node(int x, int y, int g = 0, int h = 0, Node* parent = nullptr)
        : x(x), y(y), g(g), h(h), f(g + h), parent(parent) {}
};

网格

int n; // 网格大小
cout << "请输入网格大小N: ";
cin >> n;
vector<vector<int>> grid(n, vector<int>(n, 0)); // 初始化网格，0表示通路，1表示障碍

启发式函数

// 启发式函数，使用曼哈顿距离作为函数值h
int heuristic(int x1, int y1, int x2, int y2) {
    return abs(x1 - x2) + abs(y1 - y2);
}

其他功能

随机生成障碍物

int obstacles;
cout << "请输入障碍数量: ";
cin >> obstacles;
for (int i = 0; i < obstacles; ++i) {
    int x = rand() % n;
    int y = rand() % n;
    // 确保起点、终点和已设置的障碍物位置不会重复
    if (grid[x][y] == 1 || (x == 0 && y == 0) || (x == n - 1 && y == n - 1)) {
        --i; // 遇到重复障碍物位置则重新生成
        continue;
    }
    grid[x][y] = 1; // 设置障碍物
}

检查下一格是否能通行

// 检查当前节点是否能通行（越界、障碍物检测）
bool isAvailable(int x, int y, const vector<vector<int>>& grid, int n) {
    return (x >= 0 && x < n && y >= 0 && y < n && grid[x][y] == 0);
}

比较器

// 比较器，用于优先队列，保证节点f值越小优先级越高
struct Compare {
    bool operator()(const Node* a, const Node* b) {
        return a->f > b->f;
    }
};

A*算法流程

// A*算法主流程
vector<PII> aStar(const vector<vector<int>>& grid, int n) {
    // 初始化起点和终点
    Node* start = new Node(0, 0, 0, heuristic(0, 0, n - 1, n - 1));
    Node* goal = new Node(n - 1, n - 1);

    priority_queue<Node*, vector<Node*>, Compare> openList;  // OPEN表：优先队列，用于存储待处理的节点，f值小的节点优先
    unordered_set<int> closedList;  // CLOSED表，使用哈希表存储已访问节点
    openList.push(start);  // 将起点加入OPEN表

    // 定义上下左右四个方向，用于遍历邻居节点
    vector<PII> directions = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };

    // A*算法主循环
    while (!openList.empty()) {
        // 处理OPEN表中f值最小的节点
        Node* current = openList.top();
        openList.pop();

        // 将当前节点标记为已访问，为每个坐标生成一个唯一的整数键 x*n+y
        closedList.insert(current->x * n + current->y);

        // 检查是否到达目标点
        if (current->x == goal->x && current->y == goal->y) {
            // 如果到达目标点，则回溯路径并返回
            vector<PII> path;
            while (current) {
                path.push_back({ current->x, current->y });
                current = current->parent;
            }
            //reverse(path.begin(), path.end());
            return path;
        }

        // 遍历当前节点的四个方向上的邻居节点
        for (auto& d : directions) {
            int nx = current->x + d.x;
            int ny = current->y + d.y;

            // 检查邻居节点是否能够通行，且未被访问过
            if (isAvailable(nx, ny, grid, n) && closedList.find(nx * n + ny) == closedList.end()) {
                int g = current->g + 1; // 计算从起点到邻居节点的代价
                int h = heuristic(nx, ny, goal->x, goal->y); // 估算从邻居节点到目标节点的代价
                openList.push(new Node(nx, ny, g, h, current)); // 将该邻居节点指向父节点，并加入开放列表
            }
        }
    }

    // 如果未找到路径，返回空路径
    return {};
}

实验结果

模糊推理：无人车车速规划

算法流程

1. 模糊逻辑的建立

模糊集合

• 输入变量：

  • 曲率：小、中、大**（这里只考虑上下左右四个方向的移动，所以曲率统一只有 0 和 1！）**
  • 障碍物距离：近、中、远

• 输出变量：

  • 车辆速度：慢(30km/h)、中(60km/h)、快(100km/h)

隶属函数

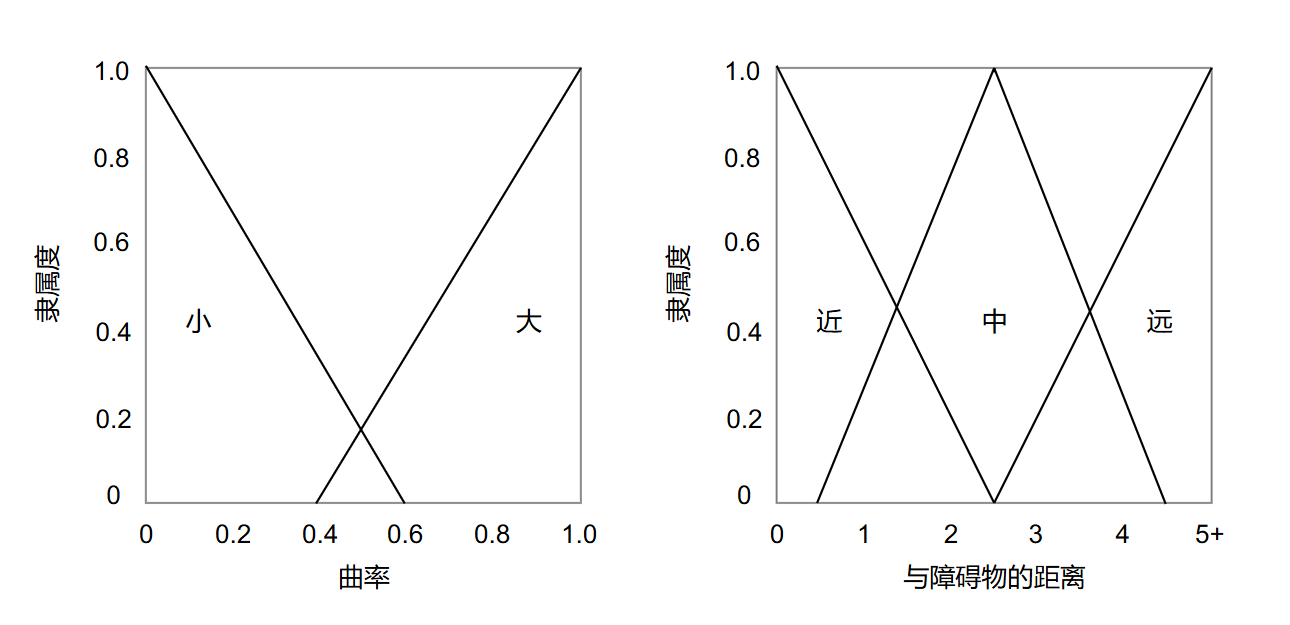
以 Zadeh 表示法，隶属函数定义如下：

曲率：

障碍物距离：

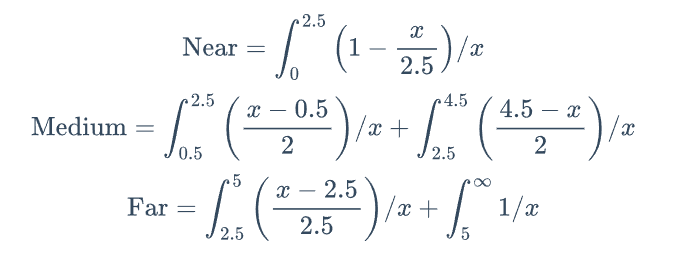
2. 模糊规则和关系矩阵的建立

（1）模糊规则

基于专家经验，通过 IF-THEN 语句建立以下 9 条规则：

• 如果曲率小且距离近，则速度中
• 如果曲率小且距离中，则速度快
• 如果曲率小且距离远，则速度快
• 如果曲率大且距离近，则速度慢
• 如果曲率大且距离中，则速度慢
• 如果曲率大且距离远，则速度中

每条规则对应输入到输出的模糊关系。

（2）模糊关系矩阵

将模糊规则转化为关系矩阵，表示输入变量的模糊集合到输出变量的模糊集合的映射。

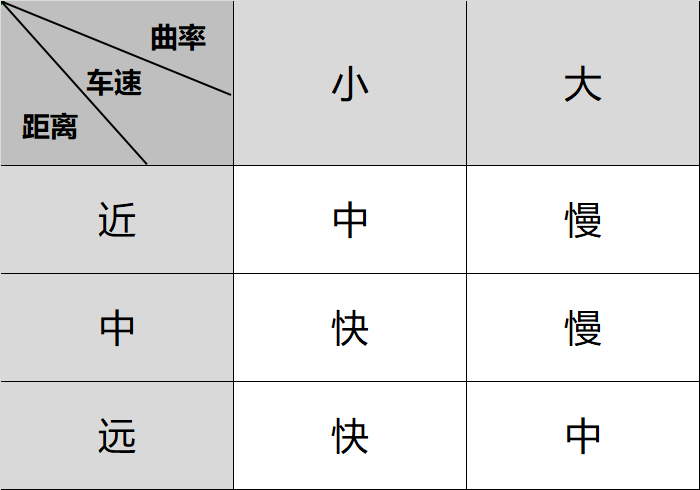
3. 模糊推理与清晰化

1. 输入变量模糊化：使用隶属函数，计算每个输入集合的隶属度值。

2. 计算模糊控制规则的强度：遍历所有规则，计算规则激活程度，激活程度等于模糊关系矩阵中对应组合条件的隶属度的最小值（最小算子运算）。

   例子：

   若规则a：曲率大，障碍物距离近 --> 车速慢

   • 曲率对“大”隶属度为0.1，障碍物距离对“近”隶属度为0.075，则 规则a的激活程度 = min(0.1, 0.075) = 0.075

3. 确定模糊输出：使用最大值法，合成所有规则对每个输出模糊集合的贡献，计算出输出模糊集合的隶属度值。

   例子：

   假设贡献了“车速慢”的规则有以下两条：

   规则b：曲率(大)隶属度为0.53，障碍物距离(中)隶属度为0.467 --> 车速慢。激活程度 = min(0.53, 0.467) = 0.467

   规则c：曲率(中)隶属度为0.10，障碍物距离(近)隶属度为0.467 --> 车速慢。激活程度 = min(0.10, 0.467) = 0.1

   最终，“车速慢"的隶属度是规则b和规则c激活程度的较大者 0.467

4. 去模糊化：使用加权平均判决法进行去模糊化。

   例子：

   • 车速慢的隶属度：0.467
   • 车速中的隶属度：0.075
   • 车速快的隶属度：0

   使用加权平均判决法计算最终车速得：

   v = (0.467 * 30 + 0.075 * 60 + 0 *100) / (0.467 + 0.075 + 0) = 34.15 (km/h)

模糊推理模块代码实现

class FuzzyInference {
private:
    // 定义隶属函数（曲率和障碍物距离）
    double curvatureSmall(double curvature) {
        if (curvature <= 0.6) return 1 - curvature / 0.6;
        return 0;
    }

    double curvatureLarge(double curvature) {
        if (curvature >= 0.4) return (curvature - 0.4) / 0.6;
        return 0;
    }

    double distanceNear(double distance) {
        if (distance <= 2.5) return 1 - distance / 2.5;
        return 0;
    }

    double distanceMedium(double distance) {
        if (distance > 1 && distance <= 2.5) return (distance - 0.5) / 2;
        if (distance > 2.5 && distance <= 4.5) return (4.5 - distance) / 2;
        return 0;
    }

    double distanceFar(double distance) {
        if (distance > 2.5 && distance <= 5) return (distance - 2.5) / 2.5;
        if (distance > 5) return 1.0;
        return 0;
    }

    // 计算曲率
    double computeCurvature(PII prev, PII next) {
        // 计算两段的方向向量
        int dx = abs(prev.x - next.x);
        int dy = abs(prev.y - next.y);

        // 方向变化的条件：一个水平，一个垂直
        if (dx == 1 && dy == 1) {
            return 1.0; // 曲率为 1（直角转弯）
        }
        return 0.0; // 曲率为 0（直线）
    }

    // 计算某点到最近障碍物的距离
    double computeDistance(int x, int y, const vector<vector<int>>& grid, int n) {
        // 简化版本：检查八个方向上的最小距离
        int minDist = n;
        for (int i = -1; i <= 1; ++i) {
            for (int j = -1; j <= 1; ++j) {
                if (i == 0 && j == 0) continue;
                int nx = x + i, ny = y + j;
                if (nx >= 0 && nx < n && ny >= 0 && ny < n && grid[nx][ny] == 1) {
                    minDist = min(minDist, abs(nx - x) + abs(ny - y));
                }
            }
        }
        return minDist;
    }

    // 模糊推理函数
    double fuzzyInference(double curvature, double distance) {
        // 计算输入的隶属度
        double smallCurvature = min(curvatureSmall(curvature), 1.0);
        double largeCurvature = min(curvatureLarge(curvature), 1.0);
        double nearDistance = min(distanceNear(distance), 1.0);
        double mediumDistance = min(distanceMedium(distance), 1.0);
        double farDistance = min(distanceFar(distance), 1.0);
        cout << "弧度隶属度 —— 小: " << smallCurvature << ", 大: " << largeCurvature << endl;
        cout << "距离隶属度 —— 近: " << nearDistance << ", 中: " << mediumDistance << ", 远: " << farDistance << endl;

        // 模糊规则的激活程度（最小值法）
        double rule1 = min(smallCurvature, nearDistance); // 曲率小，距离近 -> 车速中
        double rule2 = min(smallCurvature, mediumDistance); // 曲率小，距离中 -> 车速快
        double rule3 = min(smallCurvature, farDistance); // 曲率小，距离远 -> 车速快
        double rule4 = min(largeCurvature, nearDistance); // 曲率大，距离近 -> 车速慢
        double rule5 = min(largeCurvature, mediumDistance); // 曲率大，距离中 -> 车速慢
        double rule6 = min(largeCurvature, farDistance); // 曲率大，距离远 -> 车速中

        // 根据规则矩阵，输出的隶属度
        double slowSpeed = max({ rule4, rule5 });
        double mediumSpeed = max({ rule1, rule6 });
        double fastSpeed = max({ rule2, rule3 });
        cout << "车速隶属度 —— 慢: " << slowSpeed << ", 中: " << mediumSpeed << ", 快: " << fastSpeed << endl;

        // 去模糊化，计算最终车速（加权平均法）
        double speed = (slowSpeed * 30 + mediumSpeed * 60 + fastSpeed * 100) / (slowSpeed + mediumSpeed + fastSpeed);

        return speed;
    }

public:
    // 计算路径上每个点的车速
    void computeSpeeds(const vector<PII>& path, const vector<vector<int>>& grid, int n) {
        for (auto i = 1; i < path.size() - 1; ++i) {
            int x = path[i].x;
            int y = path[i].y;

            // 确定用于计算曲率的前后两点
            PII prev = { path[i - 1].x, path[i - 1].y };
            PII next = { path[i + 1].x, path[i + 1].y };
            double curvature = computeCurvature(prev, next);

            // 计算障碍物距离
            double distance = computeDistance(x, y, grid, n);

            // 使用模糊推理来计算车速
            double speed = fuzzyInference(curvature, distance);

            cout << fixed << setprecision(2) << "(" << x << "," << y << "), 曲率: " << curvature
                << ", 障碍物距离: " << distance << ", 速度: " << speed << endl << endl;
        }
    }
};

实验结果

整个程序的完整代码

#include <iostream>
#include <iomanip>
#include <vector>
#include <queue>
#include <unordered_set>
#include <cmath>
#include <algorithm>
#include <ctime>
#include <utility>
using namespace std;

#define x first
#define y second
typedef pair<int, int> PII;

// 节点结构体
struct Node {
    int x, y; // 坐标
    int g, h, f; // g为起点到当前节点的代价，h为启发式评估代价，f = g + h 为总代价
    Node* parent; // 指向父节点的指针

    Node(int x, int y, int g = 0, int h = 0, Node* parent = nullptr)
        : x(x), y(y), g(g), h(h), f(g + h), parent(parent) {}
};

class FuzzyInference {
private:
    // 定义隶属函数（曲率和障碍物距离）
    double curvatureSmall(double curvature) {
        if (curvature <= 0.6) return 1 - curvature / 0.6;
        return 0;
    }

    double curvatureLarge(double curvature) {
        if (curvature >= 0.4) return (curvature - 0.4) / 0.6;
        return 0;
    }

    double distanceNear(double distance) {
        if (distance <= 2.5) return 1 - distance / 2.5;
        return 0;
    }

    double distanceMedium(double distance) {
        if (distance > 1 && distance <= 2.5) return (distance - 0.5) / 2;
        if (distance > 2.5 && distance <= 4.5) return (4.5 - distance) / 2;
        return 0;
    }

    double distanceFar(double distance) {
        if (distance > 2.5 && distance <= 5) return (distance - 2.5) / 2.5;
        if (distance > 5) return 1.0;
        return 0;
    }

    // 计算曲率
    double computeCurvature(PII prev, PII next) {
        // 计算两段的方向向量
        int dx = abs(prev.x - next.x);
        int dy = abs(prev.y - next.y);

        // 方向变化的条件：一个水平，一个垂直
        if (dx == 1 && dy == 1) {
            return 1.0; // 曲率为 1（直角转弯）
        }
        return 0.0; // 曲率为 0（直线）
    }

    // 计算某点到最近障碍物的距离
    double computeDistance(int x, int y, const vector<vector<int>>& grid, int n) {
        // 简化版本：检查八个方向上的最小距离
        int minDist = n;
        for (int i = -1; i <= 1; ++i) {
            for (int j = -1; j <= 1; ++j) {
                if (i == 0 && j == 0) continue;
                int nx = x + i, ny = y + j;
                if (nx >= 0 && nx < n && ny >= 0 && ny < n && grid[nx][ny] == 1) {
                    minDist = min(minDist, abs(nx - x) + abs(ny - y));
                }
            }
        }
        return minDist;
    }

    // 模糊推理函数
    double fuzzyInference(double curvature, double distance) {
        // 计算输入的隶属度
        double smallCurvature = min(curvatureSmall(curvature), 1.0);
        double largeCurvature = min(curvatureLarge(curvature), 1.0);
        double nearDistance = min(distanceNear(distance), 1.0);
        double mediumDistance = min(distanceMedium(distance), 1.0);
        double farDistance = min(distanceFar(distance), 1.0);
        cout << "弧度隶属度 —— 小: " << smallCurvature << ", 大: " << largeCurvature << endl;
        cout << "距离隶属度 —— 近: " << nearDistance << ", 中: " << mediumDistance << ", 远: " << farDistance << endl;

        // 模糊规则的激活程度（最小值法）
        double rule1 = min(smallCurvature, nearDistance); // 曲率小，距离近 -> 车速中
        double rule2 = min(smallCurvature, mediumDistance); // 曲率小，距离中 -> 车速快
        double rule3 = min(smallCurvature, farDistance); // 曲率小，距离远 -> 车速快
        double rule4 = min(largeCurvature, nearDistance); // 曲率大，距离近 -> 车速慢
        double rule5 = min(largeCurvature, mediumDistance); // 曲率大，距离中 -> 车速慢
        double rule6 = min(largeCurvature, farDistance); // 曲率大，距离远 -> 车速中

        // 根据规则矩阵，输出的隶属度
        double slowSpeed = max({ rule4, rule5 });
        double mediumSpeed = max({ rule1, rule6 });
        double fastSpeed = max({ rule2, rule3 });
        cout << "车速隶属度 —— 慢: " << slowSpeed << ", 中: " << mediumSpeed << ", 快: " << fastSpeed << endl;

        // 去模糊化，计算最终车速（加权平均法）
        double speed = (slowSpeed * 30 + mediumSpeed * 60 + fastSpeed * 100) / (slowSpeed + mediumSpeed + fastSpeed);

        return speed;
    }

public:
    // 计算路径上每个点的车速
    void computeSpeeds(const vector<PII>& path, const vector<vector<int>>& grid, int n) {
        for (auto i = 1; i < path.size() - 1; ++i) {
            int x = path[i].x;
            int y = path[i].y;

            // 确定用于计算曲率的前后两点
            PII prev = { path[i - 1].x, path[i - 1].y };
            PII next = { path[i + 1].x, path[i + 1].y };
            double curvature = computeCurvature(prev, next);

            // 计算障碍物距离
            double distance = computeDistance(x, y, grid, n);

            // 使用模糊推理来计算车速
            double speed = fuzzyInference(curvature, distance);

            cout << fixed << setprecision(2) << "(" << x << "," << y << "), 曲率: " << curvature
                << ", 障碍物距离: " << distance << ", 速度: " << speed << endl << endl;
        }
    }
};

// 比较器，用于优先队列，保证节点f值越小优先级越高
struct Compare {
    bool operator()(const Node* a, const Node* b) {
        return a->f > b->f;
    }
};

// 启发式函数，使用曼哈顿距离作为函数值h
int heuristic(int x1, int y1, int x2, int y2) {
    return abs(x1 - x2) + abs(y1 - y2);
}

// 检查当前节点是否能通行（越界、障碍物检测）
bool isAvailable(int x, int y, const vector<vector<int>>& grid, int n) {
    return (x >= 0 && x < n && y >= 0 && y < n && grid[x][y] == 0);
}

// A*算法主流程
vector<PII> aStar(const vector<vector<int>>& grid, int n) {
    // 初始化起点和终点
    Node* start = new Node(0, 0, 0, heuristic(0, 0, n - 1, n - 1));
    Node* goal = new Node(n - 1, n - 1);

    priority_queue<Node*, vector<Node*>, Compare> openList;  // OPEN表：优先队列，用于存储待处理的节点，f值小的节点优先
    unordered_set<int> closedList;  // CLOSED表，使用哈希表存储已访问节点
    openList.push(start);  // 将起点加入OPEN表

    // 定义上下左右四个方向，用于遍历邻居节点
    vector<PII> directions = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };

    // A*算法主循环
    while (!openList.empty()) {
        // 处理OPEN表中f值最小的节点
        Node* current = openList.top();
        openList.pop();

        // 将当前节点标记为已访问，为每个坐标生成一个唯一的整数键 x*n+y
        closedList.insert(current->x * n + current->y);

        // 检查是否到达目标点
        if (current->x == goal->x && current->y == goal->y) {
            // 如果到达目标点，则回溯路径并返回
            vector<PII> path;
            while (current) {
                path.push_back({ current->x, current->y });
                current = current->parent;
            }
            reverse(path.begin(), path.end());
            return path;
        }

        // 遍历当前节点的四个方向上的邻居节点
        for (auto& d : directions) {
            int next_x = current->x + d.x;
            int next_y = current->y + d.y;

            // 检查邻居节点是否能够通行，且未被访问过
            if (isAvailable(next_x, next_y, grid, n) && closedList.find(next_x * n + next_y) == closedList.end()) {
                int g = current->g + 1; // 计算从起点到邻居节点的代价
                int h = heuristic(next_x, next_y, goal->x, goal->y); // 估算从邻居节点到目标节点的代价
                openList.push(new Node(next_x, next_y, g, h, current)); // 将该邻居节点指向父节点，并加入开放列表
            }
        }
    }

    // 如果未找到路径，返回空路径
    return {};
}

int main() {
    cout.setf(ios::fixed);
    cout << setprecision(2);
    int n;
    cout << "请输入网格大小N: ";
    cin >> n;

    vector<vector<int>> grid(n, vector<int>(n, 0)); // 初始化网格，0表示通路，1表示障碍

    srand(time(0)); // 设置随机种子，保证障碍物位置随机生成

    int obstacles;
    cout << "请输入障碍数量: ";
    cin >> obstacles;
    for (int i = 0; i < obstacles; ++i) {
        int x = rand() % n;
        int y = rand() % n;
        // 确保起点、终点和已设置的障碍物位置不会重复
        if (grid[x][y] == 1 || (x == 0 && y == 0) || (x == n - 1 && y == n - 1)) {
            --i; // 遇到重复障碍物位置则重新生成
            continue;
        }
        grid[x][y] = 1; // 设置障碍物
    }

    vector<PII> path = aStar(grid, n); // 执行A*算法获取最优路径

    // 将路径标记在网格上
    for (const auto& p : path) {
        if (grid[p.x][p.second] == 0) {
            grid[p.x][p.y] = 2; // 用2表示路径节点
        }
    }

    // 输出网格（这里转换了坐标系的输出形式，使其看起来是第一象限）
    cout << "生成的网格如下（■表示障碍，□表示通路，x表示路径）:\n";
    for (int i = n - 1; i >= 0; --i) {
        for (int j = 0; j < n; ++j) {
            if (grid[j][i] == 1) {
                cout << "■ ";
            }
            else if (grid[j][i] == 2 || (i == 0 && j == 0)) {
                cout << "x ";
            }
            else {
                cout << "□ ";
            }
        }
        cout << endl;
    }
    cout << endl;

    if (path.empty()) {
        cout << "无法抵达终点！" << endl;
        return 0;
    }

    FuzzyInference fi;
    fi.computeSpeeds(path, grid, n); // 开始模糊推理计算车速

    system("pause");
    return 0;
}

参考文章

• 堪称最好最全的A*算法详解（译文）
• 一文搞懂什么是模糊逻辑【附应用举例】